单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .
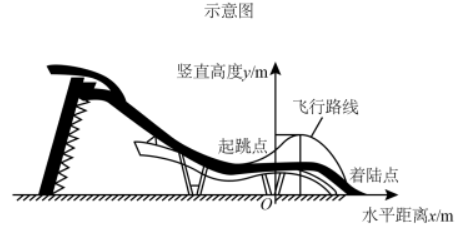
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离 与竖直高度 的几组数据如下:
水平距离 |
|
|
|
|
|
|
竖直高度 |
|
|
|
|
|
|
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系 ;
(2)第二次训练时,该运动员的竖直高度 与水平距离 近似满足函数关系 .记该运动员第一次训练的着陆点的水平距离为 ,第二次训练的着陆点的水平距离为 ,则 _____ (填“>”“=”或“<”).
某商店销售一种进价为20元/双的手套,经调查发现,该种手套每天的销售量w(双)
与销售单价x(元)满足 (20≤x≤40),设销售这种手套每天的利润为y(元).
(20≤x≤40),设销售这种手套每天的利润为y(元).(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时, 每天的利润最大?最大利润是多少?
在一个口袋中有3个完全相同的小球,把它们分别标号为1, 2, 3, 随机地摸出一个
小球记下标号后放回, 再随机地摸出一个小球记下标号, 求两次摸出小球的标号
之和等于4的概率.
已知关于x的方程(k-2)x2+2(k-2)x+k+1=0有两个实数根,求正整数k的值
如图, 在正方形网格中,△ABC的顶点和O点都在格点上.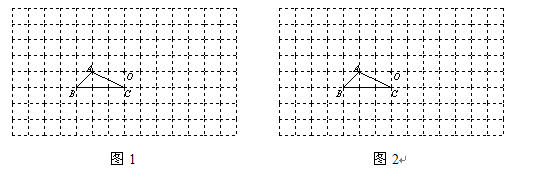
(1)在图1中画出与△ABC关于点O对称的△A′B′C′;
(2)在图2中以点O为位似中心,将△ABC放大为原来的2倍(只需画出一种即可).
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x |
… |
-2 |
-1 |
0 |
1 |
2 |
… |
| y |
… |
0 |
-4 |
-4 |
0 |
8 |
… |
(1)根据上表填空:
①抛物线与x轴的交点坐标是和;
②抛物线经过点(-3, );
③在对称轴右侧,y随x增大而;(2)试确定抛物线y=ax2+bx+c的解析式.