如图,在平面直角坐标系中,抛物线 经过点 和点 ,与 轴的另一个交点为 ,与 轴交于点 ,作直线 .
(1)①求抛物线的函数表达式;
②直接写出直线 的函数表达式;
(2)点 是直线 下方的抛物线上一点,连接 交 于点 ,连接 , 的面积记为 , 的面积记为 ,当 时,求点 的坐标;
(3)点 为抛物线的顶点,将抛物线图象中 轴下方的部分沿 轴向上翻折,与抛物线剩下的部分组成新的曲线记为 ,点 的对应点为 ,点 的对应点为 ,将曲线 沿 轴向下平移 个单位长度 .曲线 与直线 的公共点中,选两个公共点记作点 和点 ,若四边形 是平行四边形,直接写出点 的坐标.

如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于点E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为ts(t>0).
(1)当t=2时,连接DE,DF,求证:四边形AEDF为菱形.
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长.
(3)是否存在某一实数t,使△PEF为直角三角形?若存在,请求出t的值;若不存在,请说明理由.
如图①,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧,满足BP=BE,连接AP,CE.
(1)求证:△ABP≌△CBE.
(2)连接AD、BD,BD与AP相交于点F,如图②.
①当 时,求证:AP⊥BD;
时,求证:AP⊥BD;
②当 (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求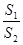 的值.
的值.
在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
请根据以上内容解答下列问题:
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点.
如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1).
(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A′B′C′与△ABC是位似图形,请写出位似中心的坐标:________;
(4)顺次连接C、C1、C′、C2,所得到的图形是轴对称图形吗?
已知:如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.