综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平;
操作二:在 上选一点 ,沿 折叠,使点 落在矩形内部点 处,把纸片展平,连接 .
根据以上操作,当点 在 上时,写出图1中一个 的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片 按照(1)中的方式操作,并延长 交 于点 ,连接 .
①如图2,当点 在 上时, ______ , ______ ;
②改变点 在 上的位置(点 不与点 重合),如图3,判断 与 的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片 的边长为 ,当 时,直接写出 的长.

已知:a2﹣b2=(a﹣b)(a+b);a3﹣b3=(a﹣b)(a2+ab+b2);a4﹣b4=(a﹣b)(a3+a2b+ab2+b3);按此规律,则:
(1)a5﹣b5=(a﹣b)( _________ );
(2)若a﹣ =2,你能根据上述规律求出代数式a3﹣
=2,你能根据上述规律求出代数式a3﹣ 的值吗?
的值吗?
求值:(2+1)•(22+1)•(24+1)•(28+1)•(216+1)﹣232.
利用平方差公式计算99992.
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
如图,一个边长为1的正方形,依次取正方形的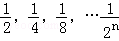 ,根据图示我们可以知道:第一次取走
,根据图示我们可以知道:第一次取走 后还剩
后还剩 ,即
,即 =1﹣
=1﹣ ;前两次取走
;前两次取走 +
+ 后还剩
后还剩 ,即
,即 +
+ =1﹣
=1﹣ ;前三次取走
;前三次取走 +
+ +
+ 后还剩
后还剩 ,即
,即 +
+ +
+ =1﹣
=1﹣ ;…前n次取走后,还剩 _________ ,即 _________ = _________ .
;…前n次取走后,还剩 _________ ,即 _________ = _________ .
利用上述计算:
(1) = _________ .
= _________ .
(2) = _________ .
= _________ .
(3)2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012(本题写出解题过程)
“*”是规定的一种运算法则:a*b=a2﹣b.
①求5*(﹣1)的值;
②若3*x=2,求x的值;
③若(﹣4)*x=2+x,求x的值.