如图,小睿为测量公园的一凉亭 的高度,他先在水平地面点 处用高 的测角仪DE测得 ,然后沿 方向向前走 到达点 处,在点 处用高 的测角仪 测得 .求凉亭 的高度.( 三点共线, .结果精确到 )

(参考数据: )
.如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.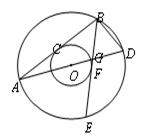
(1)求BD的长;
(2)求∠ABE+2∠D的度数.
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为 ,向左转和直行的频率均为
,向左转和直行的频率均为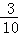 .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为 .
.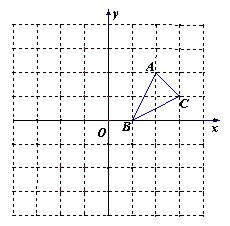
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针方向旋转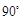 所得的△A2B2C2;
所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称吗?若成轴对称,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB
是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,ΔABC还需满足什么条件,点E才一定是AC的中点?(直接写出
结论).
某公园出售的一次性使用门票,每张10元,为了吸引更多游客,新近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分A、B两类:
A类年票每张100元,持票者每次进入公园无需再购买门票;
B类年票每张50元,持票者进入公园时需再购买每次2元的门票.
(1)某游客中一年进入该公园共有n次,
如果不购买年票,则一年的费用为元;
如果购买A类年票,则一年的费用为元;
如果购买B类年票,则一年的费用为元;(用含n的代数式表示)
(2)假如某游客一年中进入该公园共有12次,选择哪种购买方式比较优惠?请通过计算说明理由.
(3)某游客一年中进入该公园n次,他选择购买哪一类年票合算?请你帮助他决策,
并说明你的理由.