在平面直角坐标系xoy中，抛物线ymx22mx3m≠0与x轴-优题课

题文

在平面直角坐标系 $xoy$ 中，抛物线 $y = m x^{2} - 2 mx - 3 (m \neq 0)$ 与 $x$ 轴交于 $A (3, 0), B$ 两点.

（1）求抛物线的解析式及点 $B$ 的坐标；

（2）当 $- 2 < x < 3$ 时的函数图象记为 $G$ ，求此时函数 $y$ 的取值范围；

（3）在（2）的条件下，将图象 $G$ 在 $x$ 轴上方的部分沿 $x$ 轴翻折，图象 $G$ 的其余部分保持不变，得到一个新图象 $M$ .若经过 $C (4, 2)$ 点的直线 $y = kx + b (k \neq 0)$ 与图象 $M$ 在第三象限内有两个公共点，结合图象，求 $b$ 的取值范围.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

（广元）如图，AB是⊙O的弦，D为半径OA的中点．过D作CD⊥OA交弦AB于点E，交⊙O于点F．且CE=CB．
（1）求证：BC是⊙O的切线；
（2）连接AF、BF，求∠ABF的度数；
（3）如果CD=15，BE=10，sinA=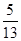．求⊙O的半径．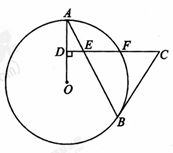

（绵阳）如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于点D，连接DC，DA，OA，OC，四边形OADC为平行四边形．
（1）求证：△BOC≌△CDA；
（2）若AB=2，求阴影部分的面积．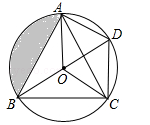

（泸州）如图，△ABC内接于⊙O，AB=AC，BD为⊙O的弦，且AB∥CD，过点A作⊙O的切线AE与DC的延长线交于点E，AD与BC交于点F．
（1）求证：四边形ABCE是平行四边形；
（2）若AE=6，CD=5，求OF的长．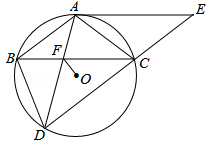

（凉山州）在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．
（1）用树状图或列表法列举点M所有可能的坐标；
（2）求点M（x，y）在函数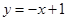的图象上的概率；
（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．

（凉山州）如图，⊙O的半径为5，点P在⊙O外，PB交⊙O于A、B两点，PC交⊙O于D、C两点．
（1）求证：PA•PB=PD•PC；
（2）若PA=，AB=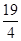，PD=DC+2，求点O到PC的距离．

试卷网试题网古诗词网作文网范文网