某海域有一小岛P，在以P为圆心，半径r为10（33）海里的圆-优题课

题文

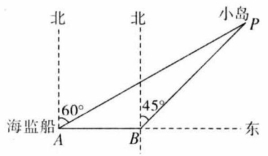
某海域有一小岛 $P$ ，在以 $P$ 为圆心，半径 $r$ 为 $10 （ 3 + \sqrt{3} ）$ 海里的圆形海域内有暗礁.一海监船自西向东航行，它在 $A$ 处测得小岛 $P$ 位于北偏东 $60^{\circ}$ 的方向上，当海监船行驶 $20 \sqrt{2}$ 海里后到达 $B$ 处，此时观测小岛 $P$ 位于 $B$ 处北偏东 $45^{\circ}$ 方向上.

（1）求 $A ， P$ 之间的距离 $AP$ ;

（2）若海监船由 $B$ 处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险，那么海监船由 $B$ 处开始沿南偏东至多少度的方向航行能安全通过这一海域?

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

在平面直角坐标系中的位置如图所示．将向右平移5个单位后再向下平移3个单位得到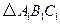

作出
写出上任意一点P(x,y)经平移后对应点为P₁的坐标
求的面积

已知：DC∥AB DF平分∠CDB ，BE平分∠ABD

求证 BE∥DF在空格处填角括号内填推理的依据
证明∵DC∥AB（已知）
∴∠ABD=
（）
又∵DF平分∠CDB BE平分∠ABD（已知）
∴∠1=∠2=（）
∴∠1=∠2（）
∴BE∥DF（）

已知：在△ABC中 ∠A =∠B =2∠C，求各内角的度数并判断△ABC的形状

甲、乙两人准备在一段长为1200 m的笔直公路上进行跑步，甲、乙跑步的速度分别为4 和 6 ，起跑前乙在起点，甲在乙前面100 m处，若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲、乙两人之间的距离y（m）与时间t（s）的函数图像是（）

如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．

（1）在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；
（2）在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．

试卷网试题网古诗词网作文网范文网