已知平面直角坐标系中,点 和直线 (其中 不全为0 ,则点 到直线 的距离 可用公式 来计算.
例如:求点 到直线 的距离,因为直线 可化为 ,其中 ,所以点 到直线 的距离为 .根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)在(1)的条件下, 的半径 ,判断 与直线 的位置关系,若相交,设其弦长为 ,求 的值;若不相交,说明理由.
在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.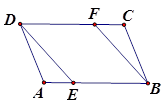
(1)求证:△ADE≌△CBF;
(2)若DF=BF,试判定四边形DEBF是何种特殊四边形?并说明理由.
(1)计算: ;(2)用配方法解方程:x2-2x-1=0.
;(2)用配方法解方程:x2-2x-1=0.
已知抛物线的解析式为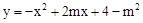
(1)求证:不论m为何值,此抛物线与x轴必有两个交点,且两交点A、B之间的距离为定值;
(2)设点P为此抛物线上一点,若△PAB的面积为8,求符合条件的点P的坐标;
(3)若(2)中△PAB的面积为S(S>0),试根据面积S值的变化情况,确定符合条件的点P的个数(本小题直接写出结论,不要求写出计算、证明过程).
如图,△ABC的两条高AD、CE相交于点H,D、E分别是垂足,过点C作BC的垂线交△ABC的外接圆于点F,求证:AH=FC.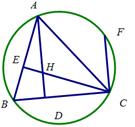
已知抛物线 (m是常数,
(m是常数,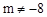 )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
(1)此抛物线的解析式;
(2)求点A、B、C的坐标.