如图所示,在 中, 为 边上一点, 是方程 的一个较大的根,求 的长

在直角坐标系中,将坐标(0,0)、(0,4)、(2,0)、 (4,4)的点用线段依次连接起来,形成一个图形.
(1)在直角坐标系中画出该图形,并说明该图形是什么形状?
(2)若每个点的纵坐标不变,横坐标分别乘以-1,则所得图形与原图形有什么关系?
已知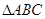 及其外一点
及其外一点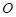 ,画出
,画出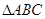 绕点
绕点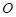 按顺时针方向旋转90°后的图形
按顺时针方向旋转90°后的图形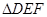 ,写出所有的旋转角.(保留作图痕迹,不写画法)
,写出所有的旋转角.(保留作图痕迹,不写画法)
某小组进行英语口语测试,测试成绩(满分10分)的统计结果如下表.
求:(1)这组学生英语口语成绩的平均分是多少?
(2)这组英语口语成绩的众数、中位数分别是多少?
| 成绩/分 |
5 |
7 |
8 |
9 |
10 |
| 人数 |
1 |
1 |
3 |
4 |
6 |
如图,已知 ,点
,点 都在格点上.
都在格点上.
(1)求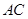 的长;
的长;
(2)若将 向右平移2个单位得到
向右平移2个单位得到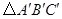 ,求
,求 点的对应点
点的对应点 的坐标;
的坐标;
(3)在坐标系中标出点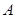 关于坐标原点对称的点
关于坐标原点对称的点 ,并写出点
,并写出点 的坐标.
的坐标.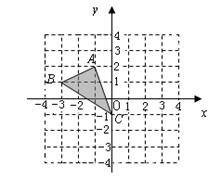
化简: