如图①，在四边形ABCD中，ABCD，E，F分别是BC，AD-优题课

题文

如图①，在四边形 $ABCD$ 中， $AB = CD ， E ， F$ 分别是 $BC ， AD$ 的中点，连接 $EF$ 并延长，分别与 $BA ， CD$ 的延长线交于点 $M ， N$ ，则 $∠ BME = ∠ CNE$ .

（温馨提示：在图①中，连接 $BD$ ，取 $BD$ 的中点 $H$ ，连接 $HE ， HF$ ，根据三角形中位线定理，证明 $HE = HF$ ，从而 $∠ 1 = ∠ 2$ ，再利用平行线性质，可证 $∠ BME = ∠ CNE$ .）

（1）如图②，在四边形 $ADBC$ 中， $AB$ 与 $CD$ 相交于点 $O ， AB = CD ， E ， F$ 分别是 $BC ， AD$ 的中点，连接 $EF$ ，分别交 $DC ， AB$ 于点 $M ， N$ ，判断 $△ OMN$ 的形状，并给予证明；

（2）如图③，在 $△ ABC$ 中， $AC > AB ， D$ 点在 $AC$ 上， $AB = CD ， E ， F$ 分别是 $BC ， AD$ 的中点，连接 $EF$ 并延长，与 $BA$ 的延长线交于 $G$ ，若 $∠ EFC = 60^{\circ}$ ，连接 $GD$ ，判断 $△ AGD$ 的形状并证明.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

如图1，某超市从一楼到二楼的电梯AB的长为16.50米，坡角∠BAC为32°。

（1）求一楼于二楼之间的高度BC（精确到0.01米）；
（2）电梯每级的水平级宽均是0.25米，如图2．小明跨上电梯时，该电梯以每秒上升2级的高度运行，10秒后他上升了多少米（精确到0.01米）？备用数据：sin32°=0.5299，con32°=0.8480，tan32°=6249。

如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M。

（1）若∠ACD=114°，求∠MAB的度数；
（2）若CN⊥AM，垂足为N，求证：△ACN≌△MCN。

（1）计算：；（2）解不等式组：。

如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax²+bx+c经过O、A、C三点．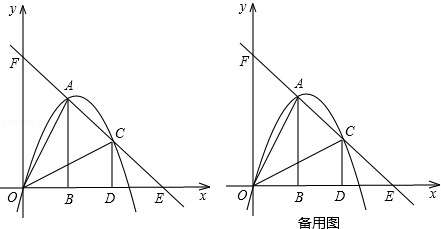

（1）求该抛物线的函数解析式；
（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

课本中，把长与宽之比为的矩形纸片称为标准纸．请思考解决下列问题：
（1）将一张标准纸ABCD（AB＜BC）对开，如图1所示，所得的矩形纸片ABEF是标准纸．请给予证明．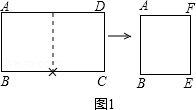

（2）在一次综合实践课上，小明尝试着将矩形纸片ABCD（AB＜BC）进行如下操作：
第一步：沿过A点的直线折叠，使B点落在AD边上点F处，折痕为AE（如图2甲）；
第二步：沿过D点的直线折叠，使C点落在AD边上点N处，折痕为DG（如图2乙），此时E点恰好落在AE边上的点M处；
第三步：沿直线DM折叠（如图2丙），此时点G恰好与N点重合．

请你探究：矩形纸片ABCD是否是一张标准纸？请说明理由．
（3）不难发现：将一张标准纸按如图3一次又一次对开后，所得的矩形纸片都是标准纸．现有一张标准纸ABCD，AB=1，BC=，问第5次对开后所得标准纸的周长是多少？探索直接写出第2012次对开后所得标准纸的周长．

试卷网试题网古诗词网作文网范文网