阅读下面的材料:
例1:求函数 的反函数;
解:由 ,可得 ,所以原函数 的反函数是 .
例2求函数 的反函数.
解:由 ,可得 ,所以原函数 的反函数是 .
以上两例中,在相应的条件下,一个原函数有反函数时,原函数中自变量 的取值范围就是它的反函数中函数值 的取值范围,原函数中函数值 的取值范围就是它的反函数中自变量 的取值范围,通过以上内容完成下面任务.
(1)求函数 的反函数;
(2)函数 的反函数的函数值的取值范围为_____;
| A. |
|
B. |
|
C. |
|
D. |
|
(3)下列函数中反函数是它本身的是_____(填序号即可).
① ;② ;③ ;④ ;⑤
先化简,再求值: ,其中x=
,其中x= .
.
解不等式组 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
计算:
如图,已知平面直角坐标系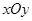 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结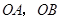 ,
,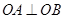 ,作
,作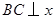 轴于
轴于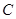 点,
点,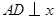 轴于
轴于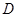 点.
点.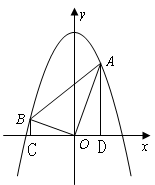
求证:mn=6
当
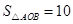 时,抛物线经过
时,抛物线经过 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式在(2)的条件下,设直线
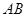 交
交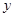 轴于点
轴于点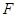 ,过点
,过点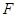 作直线
作直线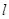 交抛物线于
交抛物线于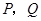 两点,问是否存在直线
两点,问是否存在直线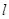 ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线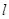 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
随着生活水平的逐步提高,某单位的私家小轿车越来越多,为确保有序停车,单位决定筹集资金维修和新建一批停车棚.该单位共有42辆小轿车,准备维修和新建的停车棚共有6个,费用和可供停车的辆数及用地情况如下表:
| 停车棚 |
费用(万元/个) |
可停车的辆数(辆/个) |
占地面积(m2/个) |
| 新建 |
4 |
8 |
100 |
| 维修 |
3 |
6 |
80 |
已知可支配使用土地面积为580m2,若新建停车棚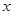 个,新建和维修的总费用为
个,新建和维修的总费用为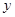 万元.
万元.求
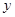 与
与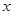 之间的函数关系
之间的函数关系满足要求的方案有几种?
为确保工程顺利完成,单位最少需要出资多少万元