如图,已知直线 在 上,且满足 平分 .
(1)求 的度数;
(2)若平行移动 ,那么 的值是否随之发生变化?若变化,找出规律;若不变,求出这个比值;
(3)在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出其度数;若不存在,说明理由.

某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为190次一组的频率为0.12.(说明: 组中值为190次的组别为 180≤次数<200)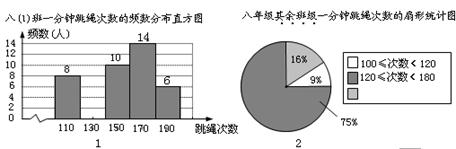
请结合统计图完成下列问题:
(1)八(1)班的人数是,组中值为110次一组的频率为;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连结DE。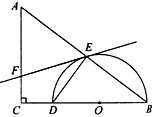
(1)当BD=3时,求线段DE的长;
(2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.
求证:△FAE是等腰三角形.
已知:如图,在平面直角坐标系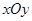 中,直线AB分别与
中,直线AB分别与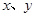 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,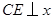 轴于点E,
轴于点E,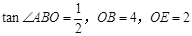 ..
..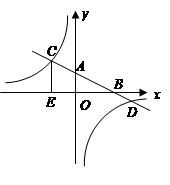
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
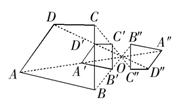
请把如图所示的图形放大2倍.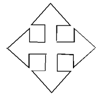
如图,四边形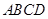 和四边形
和四边形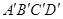 ′位似,位似比
′位似,位似比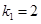 ,四边形
,四边形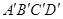 和四边形
和四边形 位似,位似比
位似,位似比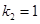 .四边形
.四边形 和四边形
和四边形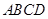 是位似图形吗?位似比是多少?
是位似图形吗?位似比是多少?