一只青蛙在平面直角坐标系上从点 开始,可以按照如下两种方式跳跃:①能从任意一点 ,跳到点 或 ;②对于点 ,如果 ,则能从 跳到 ,如果 ,则能从 跳到 ,例如,按照上述跳跃方式,这只青蛙能够到达点 ,跳跃的一种路径为: ,请你思考:这只青蛙按照规定的两种方式跳跃,能达到下列各点吗?如果能,请分别给出从点 出发到指定点的路径;如果不能,请说明理由.
(1) ;(2) ;(3) ;(4) .
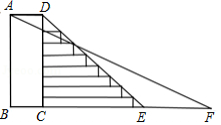
为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形 为矩形, ,其坡度为 ,将步梯 改造为斜坡 ,其坡度为 ,求斜坡 的长度.(结果精确到0.01 ,参考数据: ,
生死守护,致敬英雄.湘潭28名医护人员所在的湖南对口支援湖北黄冈医疗队红安分队,精心救治每一位患者,出色地完成了医疗救治任务.为致敬英雄,某校音乐兴趣小组根据网络盛传的"红旗小姐姐"跳的儋州调声组建了舞蹈队.现需要选取两名学生作为舞蹈队的领舞,甲、乙两班各推荐了一男生和一女生.(温馨提示:用男 、女 ;男 、女 分别表示甲、乙两班4个学生)
(1)请用列举的方法写出所有可能出现的结果;
(2)若选取的两人来自不同的班级,且按甲、乙两班先后顺序选取.请用列表或画树状图的方法求出恰好选中一男一女的概率.
化简求值: ,其中 .
解分式方程: .
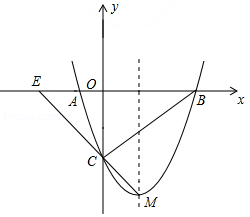
如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,点 为抛物线的顶点.
(1)求点 及顶点 的坐标.
(2)若点 是第四象限内抛物线上的一个动点,连接 、 ,求 面积的最大值及此时点 的坐标.
(3)若点 是抛物线对称轴上的动点,点 是抛物线上的动点,是否存在以点 、 、 、 为顶点的四边形是平行四边形.若存在,求出点 的坐标;若不存在,试说明理由.
(4)直线 交 轴于点 ,若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.