已知关于 的二元一次方程 ,当 每取一个值时就有一个方程,而这些方程有一个公共解,你能求出这个公共解,并证明对任何 值它都能使这个方程成立吗?
将一张矩形纸片沿对角线剪开(如图1),得到两张三角形纸片 、
、 (如
(如 图2),量得他们的斜边长为 6cm,较小锐角为30° ,再将这两张三角纸片摆成如图3的形状,且点 A、C、E、F 在同一条直线上,点 C 与点 E 重合,
图2),量得他们的斜边长为 6cm,较小锐角为30° ,再将这两张三角纸片摆成如图3的形状,且点 A、C、E、F 在同一条直线上,点 C 与点 E 重合,  保持不动,OB 为
保持不动,OB 为 的中线,现对
的中线,现对 纸片进行如下操作时遇到了三个问题,请你帮助解决.
纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的 沿CA向右平移,直到两个三角形完全重合为止.设平移距离 CE 为 x(即 CE 的长),求平移过程中,
沿CA向右平移,直到两个三角形完全重合为止.设平移距离 CE 为 x(即 CE 的长),求平移过程中, 与
与 重叠部分的面积 S 与 x 的函数关系式,以及自变量的取值范围;
重叠部分的面积 S 与 x 的函数关系式,以及自变量的取值范围;
(2)  平移到 E 与O 重合时(如图4),将
平移到 E 与O 重合时(如图4),将 绕点 O 顺时针旋转,旋转过程中
绕点 O 顺时针旋转,旋转过程中 的斜边 EF交
的斜边 EF交 的 BC 边于 G,求点 C、O、G构成等腰三角形时,
的 BC 边于 G,求点 C、O、G构成等腰三角形时, 的面积;
的面积;
(3)在(2)的旋转过程中,  的边 DE,EF分别交线段BC于点 G、H(不与端点重合).求旋转角
的边 DE,EF分别交线段BC于点 G、H(不与端点重合).求旋转角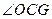 为多少度时,线段BH、GH、CG之间满足 ,
为多少度时,线段BH、GH、CG之间满足 ,  请说明理由.
请说明理由.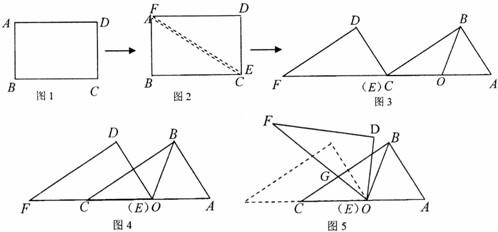
2010年8月31日,全国绿化委员会、 国 家林业局、 重庆市人民政府共同发起
家林业局、 重庆市人民政府共同发起 “绿化长江重庆行动”, 该行动就是要加快长江两岸造林绿化步伐,保护母亲河,促进入与自然和谐共生.某园艺公司从 9 月开始积极响应这一行动,进行植树造林.该公司第 x 月种植树木的亩数 y(亩)与 x 之间满足
“绿化长江重庆行动”, 该行动就是要加快长江两岸造林绿化步伐,保护母亲河,促进入与自然和谐共生.某园艺公司从 9 月开始积极响应这一行动,进行植树造林.该公司第 x 月种植树木的亩数 y(亩)与 x 之间满足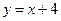 ,(其中x从9月算起,即9月时 x=l,10月时x=2,…,且
,(其中x从9月算起,即9月时 x=l,10月时x=2,…,且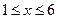 ,x为正整数).但由于植树规模增加,每亩的收益会相应降低,每亩的收益 P(千元)与种植树木亩数 y(亩)之间的关系如下表:
,x为正整数).但由于植树规模增加,每亩的收益会相应降低,每亩的收益 P(千元)与种植树木亩数 y(亩)之间的关系如下表:
| 亩数y(亩) |
5 |
6 |
7 |
8 |
… |
| 每亩收益P(千元/亩) |
46 |
44 |
42 |
40 |
… |
(1)请观察题中的表格,用所学过的一次函数、二次函数 和反比例函数的有关知识求出 P与 y 之间所 满足的函数关系表达式:
和反比例函数的有关知识求出 P与 y 之间所 满足的函数关系表达式:
(2)求该行动实施六个月来,第几月的总收益最大?此时每亩收益为多少?
(3)进入三月份,便是植树造林的“黄金期”,为 此政府出台了一项激励措施:在“植树造林”过程中, 每月植树面积与二月份植树面积相同的部分,按二月份每亩收益进行结算;超出二月份植树面积 的部分,每亩收益将按二月份时每亩的收益再增加 0.6a%进行结算.这样,该公司三月份植树面积比二月份的植树面积增加了a%.另外,三月份时公司需对三月份之前种植的所有树木进行保养, 除去成本后政府给予每亩 5a%千元的保养补贴.最后,该公司三月份获得种植树木的收益和政府 保养补贴共 702 千元.请通过计算,估算出 a 的整数值.
此政府出台了一项激励措施:在“植树造林”过程中, 每月植树面积与二月份植树面积相同的部分,按二月份每亩收益进行结算;超出二月份植树面积 的部分,每亩收益将按二月份时每亩的收益再增加 0.6a%进行结算.这样,该公司三月份植树面积比二月份的植树面积增加了a%.另外,三月份时公司需对三月份之前种植的所有树木进行保养, 除去成本后政府给予每亩 5a%千元的保养补贴.最后,该公司三月份获得种植树木的收益和政府 保养补贴共 702 千元.请通过计算,估算出 a 的整数值.
(参考数据: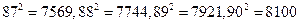 )
)
如图,在梯形 中,
中, ,
, ,
,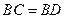 ,在
,在 上截取
上截取 ,使
,使 ,过点
,过点 作
作 于
于 ,交
,交 于点
于点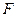 ,连接
,连接 ,交
,交 于点
于点 ,交
,交
 于点
于点 。
。
(1)求证:
(2)已知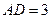 ,
, ,求
,求 的长。
的长。
为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后 得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题: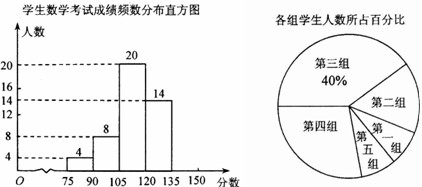

(1)本次调查共随机抽取了该年级____名学生,并将频数分布直方图补充完整:
(2)若将得分转化为等级,规定:得分低于 90分评为“D”,90~120 分评为“C”,120~135分评为 “B”,135~150分评为“A”.那么该年级 1500名考生中,考试成绩评为“B”的学生 名;
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名 学生刚好是一名女生和一名男生的概率.
如图,在平面直角坐标系 中,一次函数
中,一次函数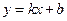 与反比例函数
与反比例函数 的图象交于点
的图象交于点 ,与
,与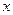 轴交于点
轴交于点 ,
, 轴于点
轴于点 ,
,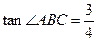 ,
, ,
,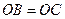 。
。
(1)求反比例函数和一次函数的解析式;
(2)若一次函数与反 比例函数的图象的另一交点为点
比例函数的图象的另一交点为点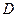 ,连接
,连接 、
、 ,求
,求