甲、乙分别自 两地同时相向步行, 后在途中相遇,相遇后,甲、乙步行速度都提高了 ,当甲到达 地后立刻按原路向 地返回.当乙到达 地后也立刻按原路向 地返回.甲、乙二人在第一次相遇后 又再次相遇,则 两地的距离是多少?
如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.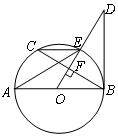
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,BC=2cm.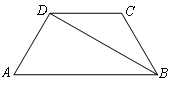
(1)求∠CBD的度数;
(2)求下底AB的长.
列方程(组)解应用题:
国家的“家电下乡”政策激活了农民购买能力,提高了农民的生活水平。“家电下乡”的补贴标准是:农户每购买一件家电,国家将按每件家电售价的13%补贴给农户.李大叔购买了一台彩电和一台洗衣机,从乡政府领到了390元补贴款.若彩电的售价比洗衣机的售价高1000元,求彩电和洗衣机的售价各是多少元.
当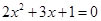 时 ,求
时 ,求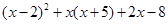 的值.
的值.
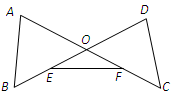
如图,已知线段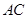 与
与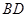 相交于点
相交于点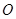 ,联结
,联结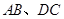 ,
,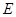 为
为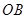 的中点,
的中点,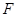 为
为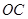 的中点,联结
的中点,联结 .若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.