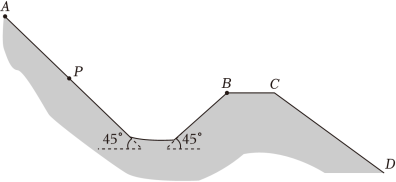
如图所示，滑雪道 由坡道和水平道组成，且平滑连接，坡道倾角均为 。平台 与缓冲坡 相连，若滑雪者从 点由静止开始下滑，恰好到达 点。滑雪者现从 点由静止开始下滑，从 点飞出。已知 、 间的距离为 ，滑雪者与滑道间的动摩擦因数均为 ，重力加速度为 ，不计空气阻力。
（1）求滑雪者运动到 点的时间 ；
（2）求滑雪者从 点飞出的速度大小 ；
（3）若滑雪者能着陆在缓冲坡 上，求平台 的最大长度 。
某一行星有一质量为m的卫星，该卫星做匀速圆周运动的周期为T，轨道半径为r，已知万有引力常量为G，求：
（1）行星的质量；
（2）卫星的加速度；
（3）若测得行星的半径恰好是卫星运行半径的
，那么行星表面的重力加速度是多少？
图甲为游乐场的悬空旋转椅，我们把这种情况抽象为图乙的模型：一质量m = 40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上，水平杆长L′= 7.5m。整个装置绕竖直杆转动，绳子与竖直方向成
角。当θ =37°时，（g = 9.8m/s2，sin37°= 0.6，cos37°= 0.8）求：
（1）绳子的拉力大小；
（2）该装置转动的角速度。
如图所示，长为l的轻细绳，上端固定在天花板上，下端系一质量为m的金属小球，将小球拉开到绳子绷直且呈水平的A点。将小球无初速度释放，求：
（1）小球落至最低点B时
的速度多大？
（2）小球落至最低点时受到的拉力.
如图所示，水平传送带以4 m/s的速度匀速运动，传送带两端A、B间的距离为20 m。现将一质量为2 kg的木块无初速地放在A端，木块与传送带间的动摩擦因数为0.2，g取10 m/s2，求木块从A端运动到B端所用的时间。
质量为3 kg的物体，在0 ~ 4 s内受水平力F的作用，在4 ~ 10 s内因受摩擦力作用而停止，其v-t图象如图所示。求：
（1）物体所受的摩擦力。
（2）在0 ~ 4 s内物体所受的拉力。
（3）在0 ~ 10 s内物体的位移。