小红家到学校有两条公共汽车线路.为了解两条线路的乘车所用时间,小红做了试验,第一周( 个工作日)选择A线路,第二周( 个工作日)选择 线路,每天在固定时间段内乘车 次并分别记录所用时间.数据统计如下:(单位: )
数据统计表
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A线路所用时间 |
15 |
32 |
15 |
16 |
34 |
18 |
21 |
14 |
35 |
20 |
|
B线路所用时间 |
25 |
29 |
23 |
25 |
27 |
26 |
31 |
28 |
30 |
24 |
根据以上信息解答下列问题:
|
平均数 |
中位数 |
众数 |
方差 |
|
|
A线路所用时间 |
22 |
a |
15 |
63.2 |
|
B线路所用时间 |
b |
26.5 |
c |
6.36 |
(1)填空:a=_____;b=_____;c=_____;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.

如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么角?
(2)∠1与∠5是内错角吗?
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
按图的方法折纸,然后回答问题:
(1)∠2是多少度?为什么?
(2)∠1与∠3有何关系?
(3)∠1与∠AEC,∠3与∠BEF分别有何关系?
如图①,∠AOB,∠COD都是直角.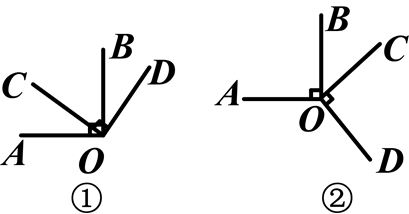
(1)试猜想∠AOD和∠BOC在数量上是否存在相等、互余或互补关系,你能说明你猜想的正确性吗?
(2)当∠COD绕点O旋转到如图②的位置时,你的猜想还成立吗?为什么?