（本题4+4分）已知关于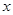的一元二次方程有两个不相等的实数根。
（1）求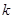的取值范围；（2）若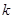为正整数，且该方程的根都是整数，求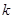的值。

（本题6+6分）
（1）计算：;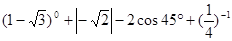
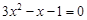（2）先化简，再求值：，其中x是方程的根．

如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（3，3）．将正方形ABCO绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．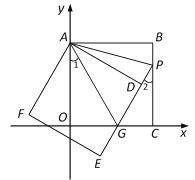

（1）求证：△AOG≌△ADG；
（2）求∠PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；
（3）当∠1=∠2时，求直线PE的解析式；
（4）在（3）的条件下，直线PE上是否存在点M，使以M、A、G为顶点的三角形是等腰三角形，若存在，请直接写出M点坐标；若不存在，请说明理由．

如图所示，AB是⊙O的直径，OC⊥AB，弦CD与OB交于点F，过圆心O作OG∥BD，交过点A所作⊙O的切线于点G，连结GD并延长与AB的延长线交于点E．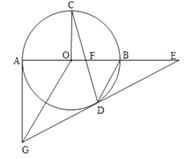

（1）求证：GD是⊙O的切线；
（2）试判断△DEF的形状，并说明理由；
（3）若OF：OB=1：3，⊙O的半径为3，求AG的长．

如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．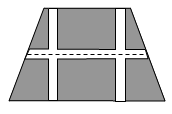

（1）用含x的式子表示横向甬道的面积为平方米；
（2）当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；
（3）根据设计的要求，甬道的宽不超过6米．如果修建甬道的总费用（万元）与甬道的宽度成正比例关系，比例系数是5．7，花坛其余部分的绿化费用为每平方米0．02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？