在甲图中，带正电粒子从静止开始经过电势差为U的电场加速后，从G点垂直于MN进入偏转磁场。该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场，磁场的磁感应强度为B，带电粒子经偏转磁场后，最终到达照相底片上的H点．测得G、H间的距离为d，粒子的重力可忽略不计。
（1）设粒子的电荷量为q，质量为m，试证明该粒子的比荷为：
；
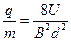（2）若偏转磁场的区域为圆形，且与MN相切于G点，如图乙所示，其它条件不变。要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上（MN足够长），求磁场区域的半径应满足的条件。
(9分) 如图所示，半径为r＝0.2 m的圆柱体绕水平轴OO’以w＝9 rad / s的角速度匀速转动，把质量m＝1 Kg的物体A放在圆柱体上方，光滑竖直挡板（图中未画出）使它不能随圆柱体转动，在水平力F作用下以v＝2.4 m / s的速度向右匀速滑动，若物体A与圆柱体间的摩擦系数为m＝0.25，试求F的大小。
(10分)如图所示，滑板运动员从倾角为53°的斜坡顶端滑下，滑下的过程中他突然发现在斜面底端有一个高h=1.4m、宽L=1.2m的长方体障碍物，为了不触及这个障碍物，他必须距水平地面高度H=3.2m的A点沿水平方向跳起离开斜面。已知运动员的滑板与斜面间的动摩擦因数μ=0.1，忽略空气阻力，重力加速度g取10m/s2。（已知sin53°=0.8，cos53°=0.6）求：
（1）运动员在斜面上滑行的加速度的大小；
（2）若运动员不触及障碍物，他从斜面上起跳后到落至水平面的过程所经历的时间；
（3）运动员为了不触及障碍物，他从A点沿水平方向起跳的最小速度
(10分). 假设某星体是一个半径为R的均匀球体，已知星体的自转周期为T，在两极地表面自由落体加速度为g ；求：⑴用弹簧秤在星球表面"两极"与 "赤道"不同地点测同一物体的重力之比。⑵设想星体自转角速度加快到某一值时，在赤道上的物体会恰好自动飘起来，则此时角速度为多少？
(9分) 质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50。这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示)，木块与铁箱内壁间的动摩擦因数为μ2=0.25。设最大静摩擦力等于滑动摩擦力，取g=10m/s2。求：
(1)木块对铁箱的压力；
(2)水平拉力F的大小。
(3)缓慢减小拉力F，经过一段时间，木块落底后不反弹，某时刻当箱的速度为v=6m/s时撤去拉力，经1s时间木块从左侧到达右侧，则铁箱长度是多少？
如图所示，A、B为两块平行金属板，A板带正电、B板带负电。两板之间存在着匀强电场，两板间距为d、电势差为U，在B板上开有两个间距为L的小孔。C、D为两块同心半圆形金属板，圆心都在贴近B板的
处，C板带正电、D板带负电。两板间的距离很近，两板末端的中心线正对着B板上的小孔，两板间的电场强度可认为大小处处相等，方向都指向。半圆形金属板两端与B板的间隙可忽略不计。现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒（微粒的重力不计）。试问：
⑴微粒穿过B板小孔时的速度为多大？
⑵为了使微粒能在CD板间运动而不碰板，CD板间的电场强度应为多大？
⑶从释放微粒开始计时，经过多长时间微粒通过半圆形金属板间的最低点P点？