（本题12分）某一中校办工厂生产学生校服的固定成本为20000元，每多生产一件需要增加投入100元，已知总收益R（x）满足函数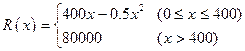
，其中x是校服的月产量，问：（1）将利润表示为关于月产量x的函数
．（2）当月产量为何值时，工厂所获利润最大?最大利润为多少元?（总收益=总成本+利润）
已知函数
.
（1）试问该函数能否在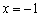
处取到极值？若有可能，求实数
的值；否则说明理由；
（2）若该函数在区间
上为增函数，求实数的取值范围.
在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组如表：
| 分组 |
频数 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
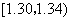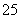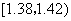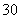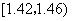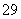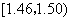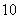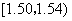| 合计 |
 |
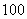（1）列出频率分布表，并画出频率分布直方图；
（2）估计纤度落在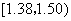
中的概率及纤度小于
的概率是多少？
（3）从频率分布直方图估计出纤度的众数、中位数和平均数．
已知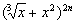
的展开式的二项式系数和比
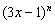的展开式的系数和大992,求
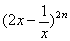的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。
已知
，其中
是自然常数，
（1）讨论
时, 
的单调性、极值；
（2）是否存在实数
，使的最小值是3，若存在，求出的值；若不存在，说明理由.
已知
在区间[0,1]上是增函数，在区间
上是减函数，又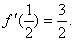
.
(1) 求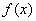
的解析式；
(2) 若在区间
(m＞0)上恒有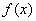≤x成立,求m的取值范围。