在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组如表：
| 分组 |
频数 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
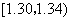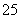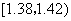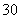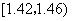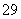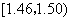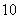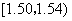| 合计 |
 |
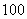（1）列出频率分布表，并画出频率分布直方图；
（2）估计纤度落在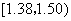
中的概率及纤度小于
的概率是多少？
（3）从频率分布直方图估计出纤度的众数、中位数和平均数．
(本题满分12分)已知向量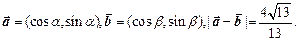
（1）求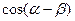
的值； （2）若
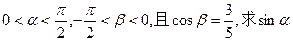的值。
（本小题满分12分）
已知不等式
为大于2的整数，
表示不超过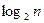
的最大整数. 设数列
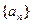的各项为正，且满足
（Ⅰ）证明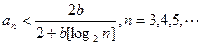
（Ⅱ）猜测数列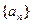是否有极限？如果有，写出极限的值（不必证明）；
（Ⅲ）试确定一个正整数N，使得当
时，对任意b>0，都有
．
（本小题满分14分）
已知直线l与椭圆
(a＞b＞0)相交于不同两点A、B,
,且
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
1). (I)求椭圆的离心率
; (II)设双曲线的离心率为
,记
,求
的解析式,并求其定义域和值域.
（本小题满分12分）已知函数
,
.
(I)证明:当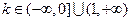
时,函数
在其定义域内为单调函数;(II)若函数的图象在点(1,
)处的切线斜率为0,且当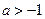
时,
≥
在
上恒成立,求实数a的取值范围.
（本小题满分12分）在长方体ABCD—A1B1C1D1中，AA1=1，AD=DC=
.（1）求直线A1C与D1C1所成角的正切值；（2）在线段A1C上有一点Q，且C1Q=
C1A1，求平面QDC与平面A1DC所成锐二面角的大小.