若函数f(x)=ax3+bx2+cx+d是奇函数,且
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
选修4—4:坐标系与参数方程在直角坐标系 中以
中以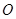 为极点,
为极点, 轴正半轴为极轴建立坐标系.圆
轴正半轴为极轴建立坐标系.圆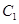 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.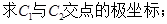
选修4—2:矩阵与变换
已知矩阵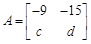 ,若矩阵
,若矩阵 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为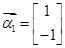 ,属于特征值1的一个特征向量为
,属于特征值1的一个特征向量为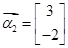 .求矩阵
.求矩阵 的逆矩阵.
的逆矩阵.
选修4—1:几何证明选讲如图,⊙ 为四边形
为四边形 的外接圆,且
的外接圆,且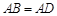 ,
,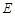 是
是 延长线上一点,直线
延长线上一点,直线 与圆
与圆 相切.
相切.
求证: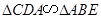 .
.
设等差数列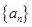 的公差为
的公差为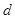 ,且
,且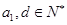 .若设
.若设 是从
是从 开始的前
开始的前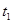 项数列的和,即
项数列的和,即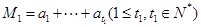 ,
, ,如此下去,其中数列
,如此下去,其中数列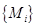 是从第
是从第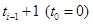 开始到第
开始到第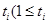 )项为止的数列的和,即
)项为止的数列的和,即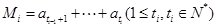 .
.
(1)若数列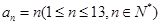 ,试找出一组满足条件的
,试找出一组满足条件的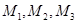 ,使得:
,使得:  ;
;
(2) 试证明对于数列 ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列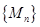 中的各数都为平方数;
中的各数都为平方数;
(3)若等差数列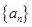 中
中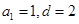 .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列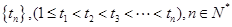 ,使得
,使得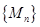 为等比数列,如存在,就求出数列
为等比数列,如存在,就求出数列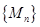 ;如不存在,则说明理由.
;如不存在,则说明理由.
本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分6分
已知函数 .
.
⑴若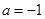 ,解方程
,解方程 ;
;
⑵若函数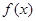 在
在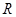 上单调递增,求实数
上单调递增,求实数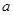 的取值范围;
的取值范围;
⑶是否存在实数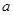 ,使不等式
,使不等式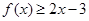 对一切实数
对一切实数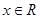 恒成立?若存在,求出
恒成立?若存在,求出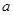 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.