设定义在R的函数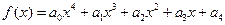 ,
,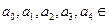 R. 当
R. 当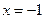 时,
时,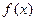 取得极大值
取得极大值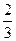 ,且函数
,且函数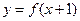 的图象关于点
的图象关于点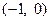 对称.
对称.
(I)求函数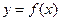 的表达式;
的表达式;
(II)判断函数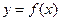 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间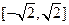 上,并说明理由;
上,并说明理由; (III)设
(III)设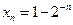 ,
,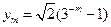 (
(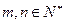 ),求证:
),求证: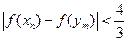 .
.
(本小题满分12分)
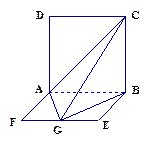 |
如图,ABCD是边长为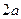 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C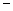 AB
AB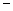 F是直二面角,
F是直二面角,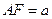 ,G是EF的中点,(Ⅰ)求证平面
,G是EF的中点,(Ⅰ)求证平面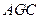 ⊥平面
⊥平面 ;
;
(Ⅱ)求GB与平面AGC所成角的正弦值.
(Ⅲ)求二面角B—AC—G的大小.
(本小题满分12分)
经统计,某大医院一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 |
0—5 |
6—10 |
11—15 |
16—20 |
21—25 |
25人以上 |
| 概率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,医院就需要增加结算窗口,请问该医院是否需要增加结算窗口?
(本小题满分12分)已知a、b、c分别是△ABC三个内角A、B、C的对边.(1)若△ABC面积为 ,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
(本小题满分12分)
(理)已知Sn是正数数列{an}的前n项和,S12,S22、……、Sn2 ……,是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.
(I)求an、bn;(II)从数列{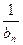 }中能否挑出唯一的无穷等比数列,使它的各项和等于
}中能否挑出唯一的无穷等比数列,使它的各项和等于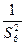 .若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
.若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。