某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为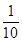 ,路段CD发生堵车事件的概率为115).
,路段CD发生堵车事件的概率为115).
(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量X,求X的概率分布.
如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD =" CD" =" 1," AA1 =" AB" =" 2," E为棱AA1的中点.
(1) 证明B1C1⊥CE;
(2) 求二面角B1-CE-C1的正弦值.
(3) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为 , 求线段AM的长.
, 求线段AM的长.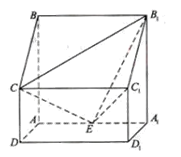
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
| 患心肺疾病 |
不患心肺疾病 |
合计 |
|
| 男 |
5 |
||
| 女 |
10 |
||
| 合计 |
50 |
已知在调查的50人中随机抽取1人,抽到患心肺疾病的人的概率为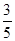 .
.
(1)请将上面的列联表补充完整;
(2)是否有 的把握认为患心肺疾病与性别有关?说明你的理由;
的把握认为患心肺疾病与性别有关?说明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,抽取3名进行其他方面的排查,记抽取患胃病的女性人数为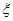 ,求
,求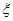 的分布列,数学期望以及方差;大气污染会引起各种疾病,试浅谈日常生活中如何减少大气污染.
的分布列,数学期望以及方差;大气污染会引起各种疾病,试浅谈日常生活中如何减少大气污染.
下面的临界值表供参考:
(参考公式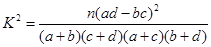 其中
其中 )
)
设函数 .
.
(1) 写出函数的最小正周期及单调递减区间;
(2) 当 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为 ,求
,求 的解析式;
的解析式;
(3) 将满足(2)的函数 的图像向右平移
的图像向右平移 个单位,纵坐标不变,横坐标伸长为原来的2倍,再向下平移
个单位,纵坐标不变,横坐标伸长为原来的2倍,再向下平移 个单位,得到函数
个单位,得到函数 ,求
,求 图像与
图像与 轴的正半轴、直线
轴的正半轴、直线 所围成图形的面积.
所围成图形的面积.
在数列{an}(n∈N*)中,已知a1=1,a2k=-ak,a2k-1=(-1)k+1ak,k∈N*. 记数列{an}的前n项和为Sn.
(1)求S5,S7的值;
(2)求证:对任意n∈N*,Sn≥0.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=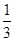 BB1,C1F=
BB1,C1F=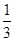 CC1.
CC1.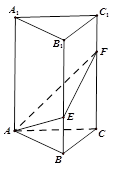
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.