（1）某实验小组用如图所示的装置测量弹簧的劲度系数k。当挂在弹簧下端的砝码处于静止状态时，测出弹簧受到的拉力F与对应的弹簧长度L（弹簧始终在弹性限度内），列表记录如下：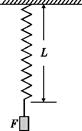
| 实验次数i |
Fi（N） |
Li（cm） |
| 1 |
0.49 |
60.20 |
| 2 |
0.98 |
61.60 |
| 3 |
1.47 |
63.05 |
| 4 |
1.96 |
64.65 |
| 5 |
2.45 |
66.10 |
| 6 |
2.94 |
67.55 |
因为逐差法常用于处理自变量等间距变化的数据组，所以小组一成员用逐差法处理数据，具体如下：将表中第三列相邻的两项求差，得出弹簧伸长量ΔL= Li - Li-1
每个ΔL都是与相同的拉力ΔF=0.49N相对应的伸长量，求出ΔL的平均值
＝＝＝cm＝1.47cm
故该弹簧的劲度系数为k＝＝＝0.333N/cm
该成员在实验数据处理中存在的问题是： ；
请你用逐差法处理表格中的数据，尽量精确计算出弹簧的劲度系数k= N/cm（结果保留三位有效数字）。
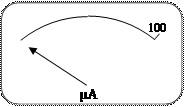
（2）一微安表
的刻度盘只标注了表示量程Ig =100μA的刻度线，尚未标注其他分刻度线，如图所示。请用下列全部器材测量微安表的内阻：
i、图示的待测微安表：内阻Rg约为2kΩ
ii、1块毫伏表
：量程250mV，最小分度5mV，内阻约为1kΩ
iii、1个滑动变阻器R1：0～50Ω
iv、1个滑动变阻器R2：0～3kΩ
v、1个直流电源E：电动势E=1.5V，内阻r约为1Ω
vi、1个单刀单掷开关S，导线若干
①在方框内画出测量微安表的内阻Rg的实验电路原理图（原理图中的元件要用相应的英文字母标注）。
②下面是主要的实验操作步骤，将所缺的内容填写在横线上方：
第一步：断开S，按电路原理图连接器材，将两个滑动变阻器R1、R2的触头分别置于合理的位置；
第二步：闭合S，分别调节R1和R2至适当位置，
③用已知量和测得量的符号表示微安表的内阻Rg=
某同学设计了一个用打点计时器探究碰撞过程中不变量的实验：在小车A的前端粘有橡皮泥，推动小车A使之做匀速运动．然后与原来静止在前方的小车B相碰并粘合成一体，继续做匀速运动，他设计的具体装置如图所示．在小车A后连着纸带，电磁打点计时器电源频率为50Hz，长木板下垫着小木片用以平衡摩擦力．
(1)若已得到打点纸带如图所示，并将测得的各计数点间距离标在图上，A点是运动起始的第一点，则应选段来计算A的碰前速度，应选段来计算A和B碰后的共同速度(以上两格填“AB”或“BC”或“CD”或“DE”)．
(2)已测得小车A的质量m1=0.40kg，小车B的质量m2=0.20kg，由以上测量结果可得：碰前mAvA+mBvB=kg·m／s；碰后mAvA’+mBvB’=kg·m／s．并比较碰撞前后两个小车质量与速度的乘积之和是否相等________。（计算结果保留三位有效数字）
⑴在做“用油膜法估测分子直径的大小”的实验中，试验简要步骤如下：
| A．将画有油膜轮廓的玻璃板放在坐标纸上，数出轮廓内的方格数（不足半个的舍去，多于半个的算一个），再根据方格的边长求出油膜的面积S。 |
| B．将一滴酒精油酸溶液滴在水面上，带油酸薄膜的形状稳定后，将玻璃板放在浅盘上，用彩笔将薄膜的形状描画在玻璃板上。 |
| C．用浅盘装入约2cm深的水，然后用痱子粉或石膏粉均匀地撒在水面上。 |
D．用公式 求出薄膜厚度，即油酸分子的大小。 |
E．根据酒精油酸溶液的浓度，算出一滴溶液中纯油酸的体积V。
F．用注射器或滴管将事先配置好的酒精油酸溶液一滴一滴地滴入量筒，记下量筒内增加一定体积时的滴数。
上述试验步骤的合理顺序是。
⑵在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为1 000 mL溶液中有纯油酸0.6 mL，用注射器测得1 mL上述溶液为80滴，把1滴该溶液滴入盛水的浅盘内，让油膜在水面上尽可能散开，测得油酸薄膜的轮廓形状和尺寸如图所示，图中正方形方格的边长为1 cm，试求：
（1）①油酸膜的面积是___________cm2；
（2）②实验测出油酸分子的直径是_________m；（结果保留两位有效数字）
（3）③实验中为什么要让油膜尽可能散开？
____________________________________________________________.
在研究平抛运动的实验中，小球必须每次从斜槽上的（1）位置落下，是为了使小球离开斜槽末端的（2）不变，同时需要调节斜槽末端（3）。在坐标纸的平抛运动轨迹上任取一点，用刻度尺量出它的坐标x和y，则实验中的小球的初速度表达式为（4）
。
右图是某同学做平抛运动实验时，用一张印有小方格的纸记录轨迹，小方格的边长L=1.25cm，若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的计算式为（5）V0=（用L、g表示），其值是（6）（取g=10m/s2）。
为了探究物体做功与物体速度变化的关系，现提供如图所示的器材，让小车在橡皮筋的作用下弹出后，沿木板滑行。请思考探究该实验的思路并回答下列问题(打点计时器交流电频率为50Hz)：
(1) 以下关于该试验的说法中有一项不正确，它是___________。
| A．本实验设法让橡皮筋对小车做的功分别为W、2W、3W、……。所采用的方法是选用同样的橡皮筋，并在每次实验中使橡皮筋拉伸的长度保持一致。当用1条橡皮筋进行是实验时，橡皮筋对小车做的功为W，用2条、3条、……橡皮筋并在一起进行第2次、第3次、……实验时，橡皮筋对小车做的功分别是2W、3W、……。 |
| B．小车运动中会受到阻力，补偿的方法，可以使木板适当倾斜。 |
| C．某同学在一次实验中，得到一条记录纸带。纸带上打出的点，两端密、中间疏。出现这种情况的原因，可能是没有使木板倾斜或倾角太小。 |
| D．根据记录纸带上打出的点，求小车获得的速度的方法，是以纸带上第一点到最后一点的距离来进行计算。 |
2) 当我们分别用相同的橡皮筋1条、2条、3条、……并起来进行第1次、第2次、第3次、……实验时，每次实验中橡皮筋拉伸的长度都应保持一致，我们把第1次实验时，橡皮筋对小车做的功为W。
（3) 由于橡皮筋对小车做功而使小车获得的速度可以由打点计时器和纸带测出，如图所示的是其中四次实验打出的部分纸带：
(4) 试根据第(2)、(3)项中的信息，完成并填写下表：
| 次数 |
1 |
2 |
3 |
4 |
| 橡皮筋对小车做的功 |
W |
2W |
3W |
4W |
| 小车速度v(m∕s) |
1.0 |
1.415 |
2.0 |
|
| 小车速度v2(m2∕s2) |
1.0 |
2.0 |
4.0 |
|
| 次数 |
1 |
2 |
3 |
4 |
| 橡皮筋对小车做的功 |
W |
2W |
3W |
4W |
| 小车速度v(m∕s) |
1.0 |
1.415 |
2.0 |
|
| 小车速度v2(m2∕s2) |
1.0 |
2.0 |
4.0 |
从表中数据可得出结论：____________________。
平抛物体的运动规律可概括为两点：①水平方向做匀速直线运动；②竖直方向做自由落体运动．为了研究平抛物体的运动，可做下面的实验，如图所示，用小锤打击弹性金属片，A球就水平飞出，同时B球被松开，做自由落体运动，两球同时落到地面，则这个实验
| A．只能说明上述规律中的第①条 |
| B．只能说明上述规律中的第②条 |
| C．不能说明上述规律中的任何一条 |
| D．能同时说明上述两条规律 |