两县城 和 相聚20km,现计划在两县城外以 为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城 和城 的总影响度为城 与城 的影响度之和,记 点到城 的距离为 ,建在 处的垃圾处理厂对城A和城B的总影响度为 ,统计调查表明:垃圾处理厂对城 的影响度与所选地点到城 的距离的平方成反比,比例系数为4;对城 的影响度与所选地点到城B的距离的平方成反比,比例系数为 ,当垃圾处理厂建在 的中点时,对称 和城 的总影响度为0.0065.
(Ⅰ)将 表示成 的函数;
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离,若不存在,说明理由。
已知椭圆 ,直线l为圆
,直线l为圆 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为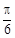 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.
(1)求e的值;
(2)试判定原点关于l的对称点是否在椭圆上,并说明理由。
已知在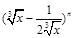 的展开式中,第6项
的展开式中,第6项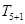 为常数项.
为常数项.
(1)求n;
(2)求展开式中所有的有理项.
某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击10次,问他最有可能射中几次?
已知函数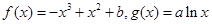 .
.
(1)若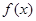 在
在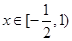 上的最大值为
上的最大值为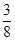 ,求实数
,求实数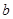 的值;
的值;
(2)若对任意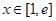 ,都有
,都有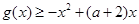 恒成立,求实数
恒成立,求实数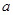 的取值范围;
的取值范围;
(3)在(1)的条件下,设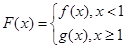 ,对任意给定的正实数
,对任意给定的正实数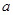 ,曲线
,曲线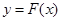 上是否存在两点
上是否存在两点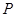 、
、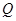 ,使得
,使得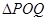 是以
是以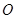 (
(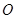 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在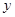 轴上?请说明理由。
轴上?请说明理由。
已知中心在坐标原点焦点在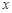 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为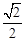 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点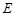 (0,1), 问是否存在直线
(0,1), 问是否存在直线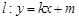 与椭圆
与椭圆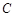 交于
交于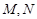 两点,且
两点,且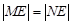 ?若存在,求出
?若存在,求出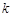 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.