按照某学者的理论,假设一个人生产某产品单件成本为
元,如果他卖出该产品的单价为
元,则他的满意度为
;如果他买进该产品的单价为
元,则他的满意度为
.如果一个人对两种交易(卖出或买进)的满意度分别为
和
,则他对这两种交易的综合满意度为
.
现假设甲生产
、
两种产品的单件成本分别为12元和5元,乙生产
、
两种产品的单件成本分别为3元和20元,设产品
、
的单价分别为
元和
元,甲买进
与卖出B的综合满意度为
,乙卖出
与买进
的综合满意度为
(1)求
和
关于
、
的表达式;当
时,求证:
=
;
(2)设
,当
、
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
,试问能否适当选取
、
的值,使得
和
同时成立,但等号不同时成立?试说明理由。
已知平行四边形ABCD(图1)中,AB=4,BC=5,对角线AC=3,将三角形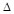 ACD沿AC折起至
ACD沿AC折起至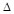 PAC位置(图2),使二面角
PAC位置(图2),使二面角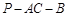 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.
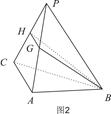
(1)求证:PC 平面BGH;
平面BGH;
(2)求平面PAB与平面BGH夹角的余弦值.
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.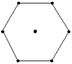
(1)求甲一次游戏中能中奖的概率;
(2)设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.
已知 ABC中,角A,B,C的对边分别为a,b,c, 若向量
ABC中,角A,B,C的对边分别为a,b,c, 若向量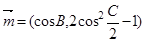 与向量
与向量 共线.
共线.
(1)求角C的大小;
(2)若 ,求a,b的值.
,求a,b的值.
已知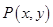 为函数
为函数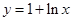 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线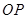 的斜率
的斜率 .
.
(Ⅰ)若函数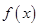 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(Ⅱ)设 ,若对任意
,若对任意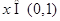 恒有
恒有 ,求实数
,求实数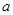 的取值范围.
的取值范围.
在平面直角坐标系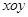 中,已知
中,已知 分别是椭圆
分别是椭圆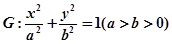 的左、右焦点,椭圆
的左、右焦点,椭圆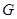 与抛物线
与抛物线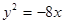 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆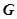 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆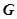 相交于
相交于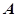 、
、 两点,若
两点,若 (
(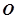 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆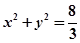 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.