设 为实数,函数 .
(1)若 ,求 的取值范围;
(2)求 的最小值;
(3)设函数 ,直接写出(不需给出演算步骤)不等式 的解集.
已知各项均为正数的数列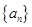 的前
的前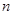 项和为
项和为 ,且对任意的
,且对任意的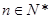 ,都有
,都有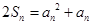 。
。
(1)求数列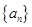 的通项公式;
的通项公式;
(2)若数列 满足
满足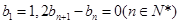 ,且cn=anbn,求数列
,且cn=anbn,求数列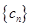 的前
的前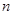 项和
项和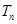 ;
;
(3)在(2)的条件下,是否存在整数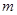 ,使得对任意的正整数
,使得对任意的正整数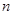 ,都有
,都有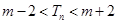 ,若存在,求出
,若存在,求出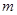 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
已知二次函数 ,不等式
,不等式 的解集为
的解集为 .
.
(1)求 的解析式;
的解析式;
(2)若函数 在
在 上单调,求实数
上单调,求实数 的取值范围;
的取值范围;
(3)若对于任意的x∈[-2,2], 都成立,求实数n的最大值.
都成立,求实数n的最大值.
某种汽车购买时费用为16.9万元,每年应交付保险费、汽油费费用共1.5万元,汽车的维修费
用为:第一年0.4万元,第二年0.6万元,第三年0.8万元,依等差数列逐年递增.
(1)设该车使用n年的总费用(包括购车费用)为 试写出
试写出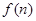 的表达式;
的表达式;
(2)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
△ABC中,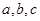 分别为角A、B、C所对的边,已知
分别为角A、B、C所对的边,已知 ,
,
(1)求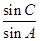 的值;
的值;
(2)若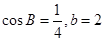 ,求△ABC的面积.
,求△ABC的面积.
等差数列 的前
的前 项和为
项和为 ,
, .
.
(1)求数列 的通项公式;(2)令
的通项公式;(2)令 ,求
,求 .
.