已知各项均为正数的数列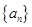 的前
的前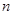 项和为
项和为 ,且对任意的
,且对任意的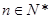 ,都有
,都有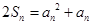 。
。
(1)求数列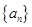 的通项公式;
的通项公式;
(2)若数列 满足
满足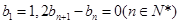 ,且cn=anbn,求数列
,且cn=anbn,求数列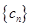 的前
的前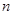 项和
项和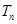 ;
;
(3)在(2)的条件下,是否存在整数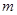 ,使得对任意的正整数
,使得对任意的正整数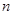 ,都有
,都有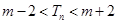 ,若存在,求出
,若存在,求出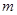 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
如图四棱锥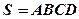 中,
中, ,
, ,
,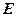 是
是 的中点,
的中点,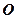 是底面正方形
是底面正方形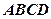 的中心,
的中心,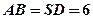 。
。
(Ⅰ)求证: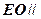 面
面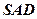 ;
;
(Ⅱ)求直线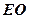 与平面
与平面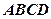 所成的角。
所成的角。
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图, 在直观图中,
在直观图中, 是
是 的中点,
的中点, 是
是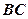 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证: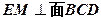 ;
;
(Ⅱ)求三棱锥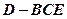 的体积。
的体积。
已知三棱锥 中,
中,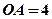 ,
, ,
, ,且
,且 两两垂直,
两两垂直, 是
是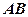 中点,
中点,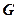 是
是 重心,现如图建立空间直角坐标系
重心,现如图建立空间直角坐标系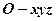 。
。
(Ⅰ)求点 和
和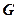 的坐标;
的坐标;
(Ⅱ)求异面直线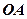 和
和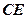 所成角的余弦值。
所成角的余弦值。
已知直线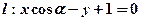 。
。
(Ⅰ)当 时,求直线
时,求直线 的斜率;
的斜率;
(Ⅱ)若直线
 的倾斜角为
的倾斜角为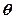 ,求
,求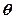 范围。
范围。
若定义在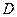 上的函数
上的函数
 满足条件:存在实数
满足条件:存在实数 且
且

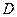 ,使得:
,使得:
⑴ 任取 ,有
,有 (
(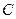 是常数);
是常数);
⑵ 对于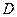 内任意
内任意 ,当
,当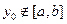 ,总有
,总有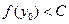 。
。
我们将满足上述两条件的函数 称为“平顶型”函数,称
称为“平顶型”函数,称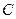 为“平顶高度”,称
为“平顶高度”,称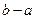 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题:
(1)函数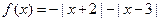 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
(2) 已知 是“平顶型”函数,求出
是“平顶型”函数,求出 的值。
的值。
(3)对于(2)中的函数 ,若
,若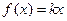 在
在 上有两个不相等的根,求实数
上有两个不相等的根,求实数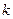 的取值范围。
的取值范围。