已知椭圆C
的离心率为
,过右焦点
的直线
与
相交于
两点,当
的斜率为1是,坐标原点
到直线
的距离为
.
(Ⅰ)求
的值;
(Ⅱ)
上是否存在点
,使得当
绕
转到某一位置时,有
成立?
若存在,求出所有的P的坐标与
的方程;若不存在,说明理由.
北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数 的分布列及数学期望
的分布列及数学期望 .
.
如图, 在矩形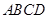 中,点
中,点 分别在线段
分别在线段 上,
上, .沿直线
.沿直线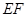 将
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四边形
将四边形 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段 的长。
的长。
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
求证:PC⊥BC;
求点A到平面PBC的距离。
如图,四棱锥S-ABCD中,SD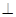 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD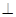 DC,
DC,
AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC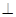 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小 .
已知三棱锥P—ABC中,PC⊥底面ABC, ,
,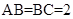 ,二面角P-AB-C为
,二面角P-AB-C为 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.
(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求直线EB与平面PAC所成的角。