已知向量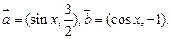
(1)当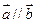 时,求
时,求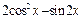 的值;(2)求
的值;(2)求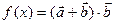 在
在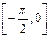 上的值域.
上的值域.

(本小题满分12分)已知动圆 过定点
过定点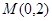 ,且在
,且在 轴上截得弦长为
轴上截得弦长为 ,设该动圆圆心的轨迹为曲线
,设该动圆圆心的轨迹为曲线
(1)求曲线 方程;
方程;
(2)点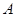 为直线
为直线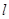 :
: 上任意一点,过
上任意一点,过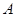 作曲线
作曲线 的切线,切点分别为
的切线,切点分别为 ,求证:直线
,求证:直线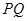 恒过定点,并求出该定点.
恒过定点,并求出该定点.
如图,正方形 所在平面与平面
所在平面与平面 垂直,
垂直, 是
是 和
和 的交点,且
的交点,且 .
.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成角的大小.
所成角的大小.
(本小题满分10分)已知中心在原点的双曲线的渐近线方程是 ,且双曲线过点
,且双曲线过点
(1)求双曲线的方程;
(2)求双曲线的焦点到渐近线的距离.
(本小题满分12分)已知数列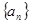 中,
中,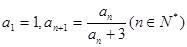 .
.
(1)求证: 是等比数列,并求
是等比数列,并求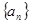 的通项公式
的通项公式 ;
;
(2)数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)在锐角△ABC中,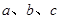 分别为∠A、∠B、∠C所对的边,且
分别为∠A、∠B、∠C所对的边,且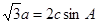
(1)确定∠C的大小;
(2)若c= ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.