（本小题满分12分）某地一水库年初有水量a(a≥10000)，其中含污染物的量为p0（设水与污染物混合均匀），已知该地降水量与月份的关系为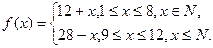
而每月流入水库的污水量与蒸发的水量都是r，且此污水中含污染物的量为p(p<r)，设当年水库中的水不作它用.
（Ⅰ）求第x月水库中水的含污比g(x)的表达式（含污比=
）；
（Ⅱ）当p0=0时，求水质量差的月份及此月的含污比.
列方程或方程组解应用题：
为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米，他从家出发到上班地点，骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍．小张用骑公共自行车方式上班平均每小时行驶多少千米?
如图，一次函数y=kx+b与反比例函数
的图象交于A（m，6），B（3，n）两点．
（1）求一次函数的解析式；
（2）根据图象直接写出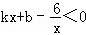
的x的取值范围；
（3）求△AOB的面积．
如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD＝3 ，AB＝5，求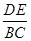
的值．
先化简，再求值： 
，其中x满足
．
解方程：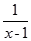
－
= 2．