列方程或方程组解应用题：
为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米，他从家出发到上班地点，骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍．小张用骑公共自行车方式上班平均每小时行驶多少千米?
（本题14分）已知不等式
的解集为
，
（
1）求实数
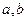的值；
（2）解关于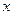
的不等式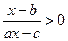
（
为实常数）
（本题12分） 若椭圆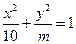
与双曲线
有相同的焦点，且椭圆与双曲线交于
点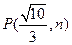
，求椭圆及双曲线的方程.
(本题12分)已知命题
；命题
表示焦点
轴上的椭圆，若
，求实数
的取值范围.
（本大题满分14分）
已知函数
，
⑴若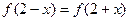
，求实数a的值？
⑵当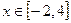
时，求函数
的最大值？
⑶当
时，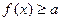
恒成立，求实
数a的最小值？
（本大题满分14分）
如图，某公园摩天轮的半径为40ｍ，圆心O距地面的高度为50ｍ，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处
（1）已知在时刻
（min）时点P距离地面的高度
，求2006min时点P距离地面的高度；
（2）当离地面（50+20
）m以上时，可以看到公园的全貌，求转一圈有多少时间可以看到公园全貌？