(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为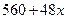 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
已知x,y的值如表所示:
| x |
2 |
3 |
4 |
| y |
5 |
4 |
6 |
如果y与x呈线性相关且回归直线方程为 ,则b=()
,则b=()
A.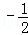 B.
B. C.
C. D.
D.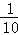
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系,对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 =kx+a,则点(a,b)与直线x+18y=100的位置关系是()
=kx+a,则点(a,b)与直线x+18y=100的位置关系是()
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
| x |
16 |
17 |
18 |
19 |
| y |
50 |
34 |
41 |
31 |
由上表,可得回归直线方程 中的
中的 =﹣4,据此模型预计零售价定为15元时,每天的销售量为()
=﹣4,据此模型预计零售价定为15元时,每天的销售量为()
A.48个 B.49个 C.50个 D.51个
已知x、y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且 =0.95x+a,则a=()
=0.95x+a,则a=()
A.1.30 B.1.45 C.1.65 D.1.80
根据如下样本数据,得到回归方程 =bx+a,则( )
=bx+a,则( )
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
﹣0.5 |
0.5 |
﹣2.0 |
﹣3.0 |
| A.a>0,b>0 |
B.a>0,b<0 |
C.a<0,b>0 |
D.a<0,b<0 |