已知函数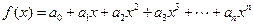
(n∈N+)，且y=f(x)的图象经过点(1，n2)，数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式；
(2)当n为奇函数时，设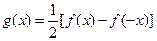
,是否存在自然数m和M，使不等式m<
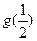<M恒成立，若存在，求出M-m的最小值；若不存在，说明理由.
．若函数y= f(2x＋1)的定义域为[ 1，2 ]，求f (x)的定义域.
已知函数f(x)的定义域为［－
，
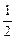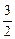］，求函数g(x)=f(3x)＋f(
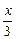)的定义域.
已知圆
，直线
．
（1）证明直线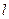
与圆相交；（2）求直线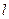被圆
截得的弦长最小时，直线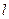的方程．
如图所示，在正方体
中，
分别是
的中点．
（1）证明：
；
（2）求
与
所成的角；
（3）证明：面
面
；
已f (
)=
，求f(x)的解析式.已知y=f(x)是一次函数，且有f [f(x)]=9x＋8，求此一次函数的解析式.
已知函数
(x)=f(x)＋g(x)，其中f(x)是x的正比例函数，g(x)是x的反比例函数，
且(
)=16，(1)=8．求
(x)的解析式，并指出定义域；求
(x)的值域.