(本题14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）
与相应的生产能耗y（吨标准煤）的几组对照数据
| ｘ |
３ |
４ |
５ |
６ |
| ｙ |
２.５ |
３ |
４ |
４.５ |
（１） 请根据上表提供的数据，求出ｙ关于ｘ的线性回归方程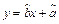
；
（２） 已知该厂技术改造前１００吨甲产品能耗为９０吨标准煤. 请进行线性相关性分析，如果有95﹪以上把握说具有线性相关性，试根据（２）求出的线性回归方程，预测生产１００吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考数据: 3×2.5+4×3+5×4+6×4.5=66.5）
| n-2 |
0.05 |
0.01 |
| 2 |
0.950 |
0.990 |
有一杯糖水，重b克，其中含糖
克，现在向糖水中再加
克糖，此时糖水变得更甜了.(其中
).
(1)请从上面事例中提炼出一个不等式(要求:①使用题目中字母;②标明字母应满足条件)
(2)利用你学过的证明方法对提炼出的不等式进行证明.
某班50名学生在一次数学测试中，成绩全部介于50与100之间，将测试结果按如下方式分成五组：第一组
，第二组
，…，第五组
．下图是按上述分组方法得到的频率分布直方图。
（Ⅰ）若成绩大于或等于60且小于80，认为合格，求该班在这次数学测试中成绩
合格的人数；
（Ⅱ）从测试成绩在
内的所有
学生中随机抽取两名同学，设其测试成绩分别为
，
，求事件“
”概率.
(1) 用辗转相除法求840与1 764的最大公约数.
(2)把“五进制”数
转化为“十进制”数，再把它转化为“八进制”数。
某市对一中学2010年高考语文和数学上线情况进行统计,随机抽查50名学生得到如下表格进行统计:统计人员甲计算数学
的观测值过程如下:
;类比甲的算法试计算语文的观测值是多少?(精确0.1)
（本小题满分10分）选修4-5：不等式选讲
已知
，且a+b+c=3，
对任意的
恒成立，求实数m的取值范围。