(本题16分)某国采用养老储备金制度,公民在就业的第一年就交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加 d(d>0), 因此,历年所交纳的储备金数目a1, a2, … 是一个公差为 d 的等差数列. 与此同时,国家给予优惠的计息政府,不仅采用固定利率,而且计算复利. 这就是说,如果固定年利率为r(r>0),那么, 在第n年末,第一年所交纳的储备金就变为 a1(1+r)n-1,第二年所交纳的储备金就变成 a2(1+r)n-2,……. 以Tn表示到第n年末所累计的储备金总额.(Ⅰ)写出Tn与Tn-1(n≥2)的递推关系式;(Ⅱ)求证Tn=An+ Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
已知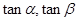 是一元二次方程
是一元二次方程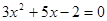 的两根,且
的两根,且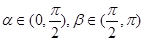 ,(1)求
,(1)求 的值;(2)求
的值;(2)求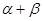 的值.
的值.
已知
(1)化简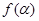 ;
;
(2)若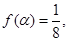 且
且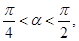 求
求 的值;
的值;
(3)求满足 的
的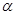 的取值集合.
的取值集合.
设函数 ,且
,且 ,
, .
.
(1)求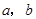 的值;
的值;
(2)当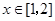 时,求
时,求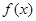 的最大值.
的最大值.
(本小题满分13分)已知椭圆的焦点在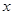 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线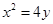 的焦点,离心率
的焦点,离心率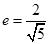 .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点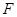 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线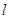 ,交椭圆于
,交椭圆于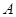 、
、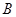 两点,设点
两点,设点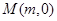 是线段
是线段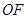 上的一个动点,且
上的一个动点,且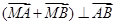 ,求
,求 的取值范围;
的取值范围;
(3)设点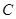 是点
是点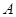 关于
关于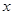 轴的对称点,在
轴的对称点,在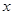 轴上是否存在一个定点
轴上是否存在一个定点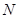 ,使得
,使得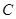 、
、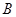 、
、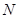 三点共线?若存在,求出定点
三点共线?若存在,求出定点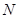 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题满分12分)函数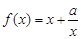 (
(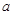 为常数)的图象过点
为常数)的图象过点 .
.
(1)求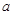 的值;
的值;
(2)函数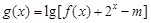 在区间
在区间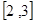 上有意义,求实数
上有意义,求实数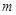 的取值范围;
的取值范围;
(3)讨论关于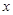 的方程
的方程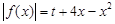 (
(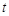 为常数)的正根的个数.
为常数)的正根的个数.