(本题16分) 设函数 ,且
,且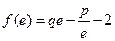 ,其中
,其中 是自然对数的底数.(1)求
是自然对数的底数.(1)求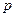 与
与 的关系;(2)若
的关系;(2)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求 的取值范围;
的取值范围;
(3)设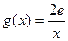 ,若在
,若在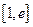 上至少存在一点
上至少存在一点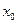 ,使得
,使得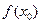 >
> 成立,求实数
成立,求实数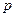 的取值范围.
的取值范围.
已知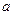 是实数,函数
是实数,函数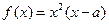
(1)若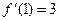 ,求
,求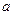 的值及曲线
的值及曲线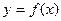 在点(1、
在点(1、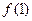 )处的切线方程。
)处的切线方程。
(2)求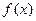 在区间[0、2]上的最大值。
在区间[0、2]上的最大值。
设函数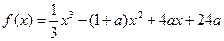 ,其中常数
,其中常数 >1。
>1。
(1)讨论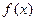 的单调性
的单调性
(2)若当 时,
时,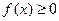 恒成立,求
恒成立,求 的取值范围。
的取值范围。
已知函数 ,当
,当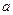 >0时,若函数
>0时,若函数 在区间[-1、2]上是减函数,求
在区间[-1、2]上是减函数,求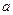 的取值范围。
的取值范围。
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为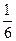 ,甲、乙、丙三位同学每人购买了一瓶该饮料。
,甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求三位同学都没有中奖的概率;
(2)求三位同学中至少有两位没有中奖的概率。
如图,在直三棱柱ABC-A1B1C1中,AB=1,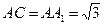 ,
,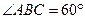
(1)证明:AB⊥A1C
(2)求二面角A-A1C-B的大小