现有10名教师,其中男教师6名,女教师4名.
(1)要从中选2名教师去参加会议,有多少种不同的选法?
(2)现要从中选出4名教师去参加会议,求男、女教师各选2名的概率.
若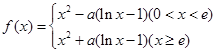 ,其中
,其中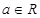 .
.
(1)当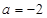 时,求函数
时,求函数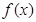 在区间
在区间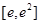 上的最大值;
上的最大值;
(2)当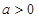 时,若
时,若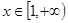 ,
,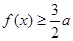 恒成立,求
恒成立,求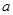 的取值范围.
的取值范围.
已知函数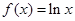 ,
,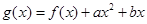 ,函数
,函数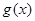 的图象在点
的图象在点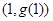 处的切线平行于
处的切线平行于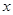 轴.
轴.
(1)确定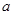 与
与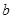 的关系;
的关系;
(2)试讨论函数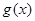 的单调性;
的单调性;
(3)证明:对任意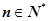 ,都有
,都有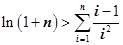 成立。
成立。
已知函数
(I)若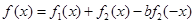 ,是否存在a,b
,是否存在a,b R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数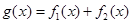 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数 成立.求a的取值范围.
成立.求a的取值范围.
已知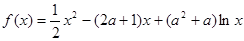 (
( ,
, 是常数),若对曲线
是常数),若对曲线 上任意一点
上任意一点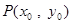 处的切线
处的切线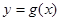 ,
,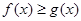 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知函数 ,函数
,函数 是函数
是函数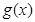 的导函数.
的导函数.
(1)若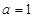 ,求
,求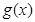 的单调减区间;
的单调减区间;
(2)若对任意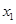 ,
, 且
且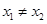 ,都有
,都有 ,求实数
,求实数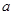 的取值范围;
的取值范围;
(3)在第(2)问求出的实数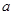 的范围内,若存在一个与
的范围内,若存在一个与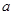 有关的负数
有关的负数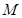 ,使得对任意
,使得对任意 时
时 恒成立,求
恒成立,求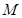 的最小值及相应的
的最小值及相应的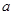 值.
值.