若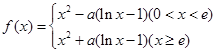 ,其中
,其中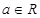 .
.
(1)当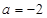 时,求函数
时,求函数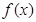 在区间
在区间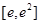 上的最大值;
上的最大值;
(2)当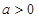 时,若
时,若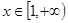 ,
,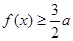 恒成立,求
恒成立,求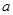 的取值范围.
的取值范围.
已知函数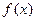 是定义在
是定义在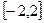 上的奇函数,当
上的奇函数,当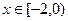 时,
时, (
( 为常数)。
为常数)。
(1)求函数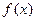 的解析式;
的解析式;
(2)当 时,求
时,求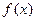 在
在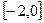 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的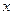 ,并猜想
,并猜想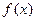 在
在 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当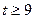 时,证明:函数
时,证明:函数 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线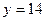 上。
上。
设函数f(x)的定义域D关于原点对称,0∈D,且存在常数a>0,使f(a)=1,又 ,
,
(1)写出f(x)的一个函数解析式,并说明其符合题设条件;
(2)判断并证明函数f(x)的奇偶性;
(3)若存在正常数T,使得等式f(x)=f(x+T)或者f(x)=f(x-T)对于x∈D都成立,则都称f(x)是周期函数,T为周期;试问f(x)是不是周期函数?若是,则求出它的一个周期T;若不是,则说明理由。
已知函数f(x)=(|x|-b)2+c,函数g(x)=x+m,
(1)当b=2,m=-4时,f(x)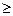 g(x)恒成立,求实数c的取值范围;
g(x)恒成立,求实数c的取值范围;
(2)当c=-3,m=-2时,方程f(x)=g(x)有四个不同的解,求实数b的取值范围.
设定义在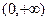 上的函数
上的函数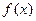 满足下面三个条件:
满足下面三个条件:
①对于任意正实数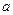 、
、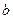 ,都有
,都有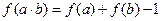 ;②
;② ;
;
③当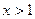 时,总有
时,总有 .
.
(1)求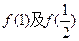 的值;
的值;
(2)求证: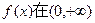 上是减函数.
上是减函数.
已知二次函数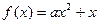 (
(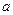
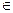 R,
R,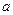
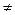 0).
0).
(Ⅰ)当0<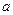 <
<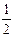 时,
时,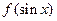 (
(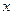
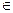 R)的最大值为
R)的最大值为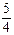 ,求
,求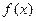 的最小值.
的最小值.
(Ⅱ)如果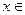 [0,1]时,总有|
[0,1]时,总有|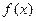 |
|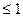 .试求
.试求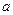 的取值范围.
的取值范围.
(Ⅲ)令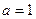 ,当
,当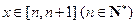 时,
时,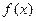 的所有整数值的个数为
的所有整数值的个数为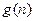 ,求数列
,求数列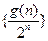 的前
的前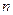 项的和
项的和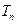 .
.