如图,在四棱锥 中,底面 四边长为1的菱形, , 底面 , , 为 的中点, 为 的中点.

(Ⅰ)证明:直线
平面
 ;
;
(Ⅱ)求异面直线
与
所成角的大小;
(Ⅲ)求点
到平面
的距离.
已知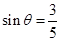 ,
,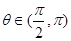 .求值:①
.求值:①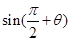 ;②
;②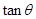 .
.
在平面直角坐标系 中,曲线C1的参数方程为
中,曲线C1的参数方程为 ,
,
( 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为 (
( ,
, 为参数),在以O为极点,
为参数),在以O为极点, 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当 时,
时,
这两个交点间的距离为 ,当
,当 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 时,l与C1,C2的交点
时,l与C1,C2的交点
分别为A2,B2,求四边形A1A2B2B1的面积.
如图,在圆内画 条线段,将圆分割成两部分;画
条线段,将圆分割成两部分;画 条相交线段,彼此分割成
条相交线段,彼此分割成 条线段,将圆分割成
条线段,将圆分割成 部分;画
部分;画 条线段,彼此最多分割成
条线段,彼此最多分割成 条线段,将圆最多分割成
条线段,将圆最多分割成 部分;画
部分;画 条线段,彼此最多分割成
条线段,彼此最多分割成 条线段,将圆最多分割成
条线段,将圆最多分割成 部分.
部分.



(1)猜想:圆内两两相交的 条线段,彼此最多分割成多少条线段?
条线段,彼此最多分割成多少条线段?
(2)记在圆内画 条线段,将圆最多分割成
条线段,将圆最多分割成 部分,归纳出
部分,归纳出 与
与 的关系.
的关系.
(3)猜想数列 的通项公式,根据
的通项公式,根据 与
与 的关系及数列的知识,证明你的猜想是否成立.
的关系及数列的知识,证明你的猜想是否成立.
设命题 :
: ,其中
,其中 ,命题
,命题 :
: ,
,
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知 ,求证:关于
,求证:关于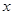 的三个方程
的三个方程 ,
,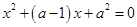 ,
,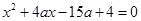 中至少有一个方程有实数根.
中至少有一个方程有实数根.