已知数列
的首项
,通项
(
为常数),且成等差数列。求:
(Ⅰ)
的值;
(Ⅱ) 数列
前
项和
的公式。
如图,四边形ABCD中, 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为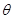 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在 内.
内.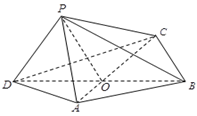
(Ⅰ)求证: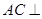 平面PBD;
平面PBD;
(Ⅱ)若已知二面角 的余弦值为
的余弦值为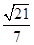 ,求
,求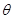 的大小.
的大小.
已知函数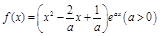
(Ⅰ)当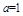 时,求函数
时,求函数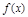 的图象在点
的图象在点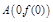 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数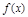 的单调性;
的单调性;
在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为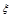 (
(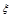 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为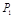 、
、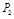 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
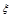 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
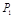 |
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
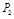 |
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
①1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
已知函数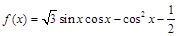 ,
,
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设 的内角
的内角 的对边分别
的对边分别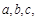 且
且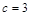 ,
, ,若
,若 求
求 的值.
的值.
设f(x)=lnx+ -1,证明:
-1,证明:
(1)当x>1时,f(x)< (x-1);
(x-1);
(2)当1<x<3时,f(x)< .
.