如图,矩形 和梯形 所在平面互相垂直, , .

(Ⅰ)求证:
平面
;
(Ⅱ)当
的长为何值时,二面角
的大小为
.
已知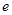 是自然对数的底数,函数
是自然对数的底数,函数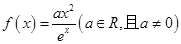 。
。
(1)求函数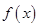 的单调递增区间;
的单调递增区间;
(2)当 时,函数
时,函数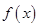 的极大值为
的极大值为 ,求
,求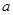 的值。
的值。
已知函数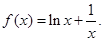
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)若g(x)=f(x)一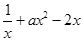 有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
(3)设q>p>2,求证:当x∈(p,q)时,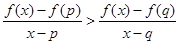 .
.
已知函数 .
.
(1)当 时,求曲线
时,求曲线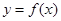 在点
在点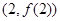 处的切线方程;
处的切线方程;
(2)当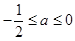 时,讨论
时,讨论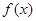 的单调性.
的单调性.
设函数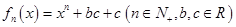 .
.
(1)设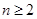 ,
,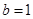 ,
,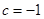 ,证明:
,证明: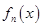 在区间
在区间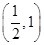 内存在唯一的零点;
内存在唯一的零点;
(2)设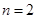 ,若对任意
,若对任意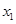 、
、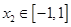 ,有
,有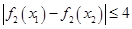 ,求
,求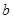 的取值范围.
的取值范围.
已知函数 ,其中
,其中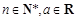 ,
,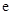 是自然对数的底数.
是自然对数的底数.
(1)求函数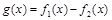 的零点;
的零点;
(2)若对任意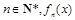 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数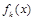 在R上是单调函数,探究函数
在R上是单调函数,探究函数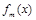 的单调性.
的单调性.