(本小题满分12分)已知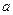 为实数,函数
为实数,函数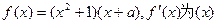 的导函数。(1)若
的导函数。(1)若 上的最大值和最小值;(2)若函数
上的最大值和最小值;(2)若函数 有两个不同的极值点,求
有两个不同的极值点,求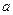 的取值范围。
的取值范围。
设函数 定义域为
定义域为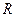 ,当
,当 时,
时, ,且对于任意的
,且对于任意的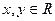 ,都有
,都有
(1)求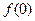 的值,并证明函数
的值,并证明函数 在
在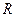 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若 时,不等式
时,不等式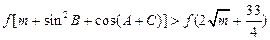 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
)设函数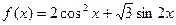 ,
,
(1)求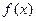 的周期以及单调增区间; (2)若
的周期以及单调增区间; (2)若 ,求sin2x的值;
,求sin2x的值;
(3)在△ABC中,a,b,c分别是角A,B,C的对边,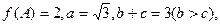 求b,c的长。
求b,c的长。
设函数
(1)求 的单调增区间和单调减区间;
的单调增区间和单调减区间;
(2)若当 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于x的方程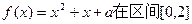 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。
设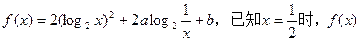 有最小值-8。
有最小值-8。
(1)求a,b;
(2)求满足 的集合A;
的集合A;
(3)若非空集合 ,求实数m的取值范围。
,求实数m的取值范围。
已知函数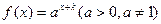 的图象过(-1,1)点,其反函数
的图象过(-1,1)点,其反函数 的图象过(8,2)点。
的图象过(8,2)点。
(1)求a,k的值;
(2)若将 的图象向在平移两个单位,再向上平移1个单位,就得到函数
的图象向在平移两个单位,再向上平移1个单位,就得到函数 的图象,写出
的图象,写出 的解析式;
的解析式;
(3)若函数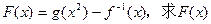 的最小值及取最小值时x的值。
的最小值及取最小值时x的值。