设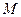 是由满足下列两个条件的函数
是由满足下列两个条件的函数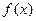 构成的集合:①方程
构成的集合:①方程 有实根; ②函数
有实根; ②函数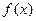 的导函数
的导函数 满足
满足 (1)判断函数
(1)判断函数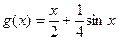 是不是集合
是不是集合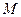 中的元素,并说明理由;(2)若集合
中的元素,并说明理由;(2)若集合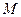 的元素
的元素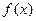 具有以下性质:“设
具有以下性质:“设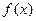 的定义域为
的定义域为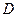 ,对于任意
,对于任意 都存在
都存在 使得等式
使得等式 成立.”试用这一性质证明:方程
成立.”试用这一性质证明:方程 只有一个实数根;(3设
只有一个实数根;(3设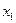 是方程
是方程 的实根,求证:对函数
的实根,求证:对函数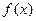 定义域中任意
定义域中任意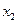 ,
,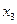 ,当
,当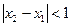 ,且
,且 时,
时,  .
.
已知{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,
(1)求数列{an}的首项a1及公差为d
(2)证明:数列{ }为等差数列并求其前n项和Tn
}为等差数列并求其前n项和Tn 。
。
在△ABC中,已知a=2 ,b=6,A=30°,解三角形.
,b=6,A=30°,解三角形.
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数 是一个随机变量,它的分布列为:
是一个随机变量,它的分布列为: ;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?
;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?
在四棱锥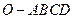 中,底面
中,底面 是边长为1的菱形,
是边长为1的菱形,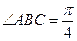 ,
,  底面
底面 ,
,  ,
,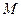 为
为 的中点
的中点
(1)求异面直线AB与MD所成角的大小;
(2)求平面 与平面
与平面 所成的二面角的余弦值.
所成的二面角的余弦值.
设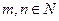 ,
,
 .
.
(1)当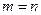 =2011时,记
=2011时,记 ,
,
求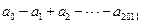 ;
;
(2)若 展开式中
展开式中 的系数是20,则当
的系数是20,则当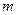 、
、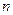 变化时,试求
变化时,试求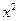 系数的最小值.
系数的最小值.