在四棱锥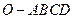 中,底面
中,底面 是边长为1的菱形,
是边长为1的菱形,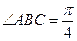 ,
,  底面
底面 ,
,  ,
,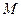 为
为 的中点
的中点
(1)求异面直线AB与MD所成角的大小;
(2)求平面 与平面
与平面 所成的二面角的余弦值.
所成的二面角的余弦值.
如图,已知椭圆 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.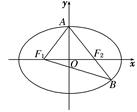
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若 =2
=2 ,
, ·
·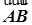 =
= ,求椭圆的方程.
,求椭圆的方程.
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 |
A |
B |
C |
D |
E |
销售额 (千万元) (千万元) |
3 |
5 |
6 |
7 |
9 9 |
利润额 (百万元) (百万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额 关于销售额
关于销售额 的回归直线方程;
的回归直线方程;
(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
如图,在底面是直角梯形的四棱锥S-ABCD中,



(1)求四棱锥S-ABCD的体积;
(2)求证:
已知{an}是一个等差数列,且a2=1,a5=-5.
(1)求数列{an}的通项an;
(2)求{an}前n项和Sn的最大值.
在△ 中,角
中,角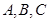 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .
.
(1)求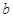 的值;
的值;
(2)求 的值.
的值.