(本小题满分14分)已知函数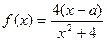 .
. (Ⅰ)判断
(Ⅰ)判断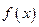 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程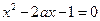 的两实根为
的两实根为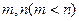 ,证明函数
,证明函数 是
是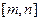 上的增函数.
上的增函数.
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中 轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为
轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为 (
( 为参数),点Q的极坐标为
为参数),点Q的极坐标为 。
。
(1)化圆C的参数方程为极坐标方程;
(2)直线 过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线
过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线 的直角坐标方程。
的直角坐标方程。
在平面直角坐标系 中,圆的参数方程为
中,圆的参数方程为 ,以坐标原点
,以坐标原点 为极点,
为极点,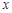 轴的正半轴为极轴建立极坐标系.求:
轴的正半轴为极轴建立极坐标系.求:
(1)圆的直角坐标方程;
(2)圆的极坐标方程.
已知直线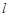 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆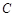 的极坐标方程为
的极坐标方程为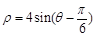 .
.
(1)求圆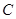 的直角坐标方程;
的直角坐标方程;
(2)若 是直线
是直线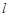 与圆面
与圆面 ≤
≤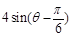 的公共点,求
的公共点,求 的取值范围.
的取值范围.
在直角坐标系 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程为
的参数方程为 .
.
(1)已知在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点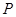 的极坐标为
的极坐标为 ,判断点
,判断点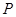 与直线
与直线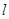 的位置关系;
的位置关系;
(2)设点 是曲线
是曲线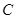 上的一个动点,求它到直线
上的一个动点,求它到直线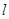 的距离的最小值.
的距离的最小值.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点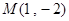 ,求|MA|·|MB|.
,求|MA|·|MB|.