一自来水厂拟建一座平面图形为矩形、面积为200平方米的净水处理池,该池的深度为1米,池的四周内壁建造单价为每平方米400元,池底建造单价为每平方米60元,在该水池长边的正中间设置一个隔层,将水池分成左右两个小水池,该隔层建造单价为每平方米100元,池壁厚度忽略不计.
(1)净水池的长度设计为多少米时,可使总造价最低?
(2)如长宽都不能超过14.5米,那么此净水池的长为多少时,可使总造价最低?
(本小题满分12分)
设函数 若
若
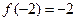 ,
,
求关于 的方程
的方程 的解集.
的解集.
(本小题满分12分)
建造一个容积为16立方米,深为4米的无盖长方体蓄水池,池壁的造价
为每平方米100元,池底的造价为每平方米200元,问怎样设计才能使
该蓄水池的总造价最低,最低造价为多少?
(本小题满分10分)
若不等式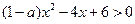 的解集是
的解集是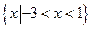 .
.
(1)解不等式 ;
;
(2)b为何值时, 的解集为R;
的解集为R;

设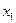 、
、
 是函数
是函数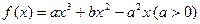 的两个极值点.
的两个极值点.
(1)若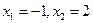 ,求函数
,求函数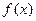 的解析式;
的解析式;
(2)若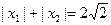 ,求
,求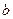 的最大值;
的最大值;
(3)设函数 ,
,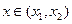 ,当
,当 时,
时,
求证:
(本题12分)
设函数 ,曲线
,曲线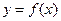 在点M
在点M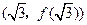 处的切线方程为
处的切线方程为 .
.
(1)求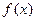 的解析式;(2)求函数
的解析式;(2)求函数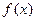 的单调递减区间;
的单调递减区间;
(3)证明:曲线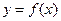 上任一点处的切线与直线
上任一点处的切线与直线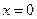 和直线
和直线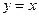 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.