(本小题满分12分)已知 的三边长
的三边长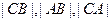 成等差数列,若点
成等差数列,若点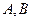 的坐标分别为
的坐标分别为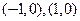 .(1)求顶点
.(1)求顶点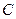 的轨迹
的轨迹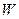 的方程;(2)若线段
的方程;(2)若线段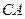 的延长线交轨迹
的延长线交轨迹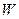 于点
于点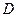 ,当
,当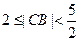 时求线段
时求线段 的垂直平分线
的垂直平分线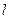 与
与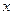 轴交点的横坐标的取值范围.
轴交点的横坐标的取值范围.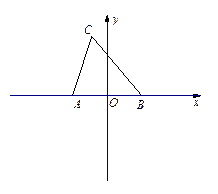
已知向量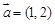 ,
,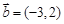 .
.
(1)求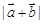 和
和 ;
;
(2)当 为何值时,
为何值时,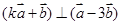 .
.
(本小题满分10分)(选修4-4:坐标系与参数方程)
在直角坐标系中,直线 的参数方程为
的参数方程为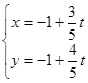
 为参数).若以坐标原点
为参数).若以坐标原点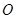 为极点,
为极点,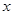 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线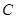 的极坐标方程为
的极坐标方程为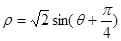 .
.
(I)求曲线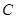 的直角坐标方程;
的直角坐标方程;
(II)求直线 被曲线
被曲线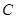 所截得的弦长.
所截得的弦长.
(本小题满分12分)
设函数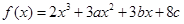 在
在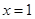 及
及 时取得极值.
时取得极值.
(I)求 的值;
的值;
(II)若对于任意的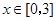 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
(本小题满分12分)
已知 是首项为
是首项为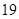 ,公差为
,公差为 的等差数列,
的等差数列, 为
为 的前
的前 项和.
项和.
(I)求通项 及
及 ;
;
(II)设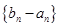 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前 项和
项和 .
.
(本小题满分12分)
某校高三年级要从 名男生
名男生 和
和 名女生
名女生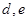 中任选
中任选 名代表参加学校的演讲比赛。
名代表参加学校的演讲比赛。
(I)求男生 被选中的概率
被选中的概率
(II)求男生 和女生
和女生 至少一人被选中的概率。
至少一人被选中的概率。