已知集合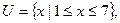
 ,
,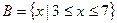 ,求:(1)
,求:(1)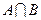 ;(2)
;(2)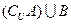
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=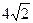 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。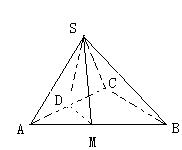
已知等腰DABC中,AC = BC = 2, ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
正方形ABCD中,以对角线BD为折线,把ΔABD折起,使二面角Aˊ-BD-C为60°,求二面角B-AˊC-D的余弦值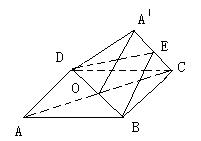
已知空间四边形ABCD中,AB =" BC" ="CD=" AD =" BD" = AC, E、F分别为AB、CD的中点,
(1)求证:EF为AB和CD的公垂线
(2)求异面直线AB和CD的距离
在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.