如图,已知 平面
平面 是正三角形,
是正三角形,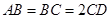 .
.
(Ⅰ)在线段 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?
?
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
已知命题p:函数y=loga(1-2x)在定义域上单调递增;命题q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若p∨q是真命题,求实数a的取值范围.
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求实数a的取值范围.
已知p:x2-8x-20≤0,q:x2-2x+1-m2≤0(m>0),若 p是
p是 q的必要不充分条件,求实数m的取值范围.
q的必要不充分条件,求实数m的取值范围.
设全集U=R,函数f(x)=lg(|x+1|+a-1)(a<1)的定义域为A,集合B={x|cosπx=1}.若(∁UA)∩B恰好有2个元素,求a的取值集合.
设全集I=R,已知集合M=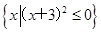 ,N={x|x2+x-6=0}.
,N={x|x2+x-6=0}.
(1)求(∁IM)∩N;
(2)记集合A=(∁IM)∩N,已知集合B={x|a-1≤x≤5-a,a∈R},若B∪A=A,求实数a的取值范围.